Какая пропорция цемента и песка для бетона?
В соответствии с принятыми строительными технологиями для строительства или заливки разных конструкций используются бетоны разных марок. К примеру, для заливки фундамента под дом необходим прочный «текучий» бетон с добавлением крупной щебенки фракцией 20-35 мм, а для формирования подушки готовят бетон плотной консистенции, как говорят «только, только» жидкий.
Состав бетона разных марок регламентируется Государственным стандартом – ГОСТ 7473-94 и Сводом Норм и Правил – СниП.5.01.23-83. При этом, необходимо учитывать влажность и плотность каждого компонента.
Только после того, как высчитаны конкретные весовые или объемные соотношения, приступают к собственно замешиванию бетона. Чтобы не утомлять читателя поиском и изучением ГОСТов и СНиПов публикуем здесь таблицу пропорций компонентов бетонов разных марок на основе самых популярных цементов М400 и М500.
Таблица пропорций бетона на основе цемента марка М400
| Марка бетона | Массовые пропорции: цемента: песка: щебенки, кг | Объемные пропорции на 10 литров цемента: песок: щебень, литры |
| М100 | 1:4,5:7 | 40:60 |
| М200 | 1:2,7:4,7 | 24:40 |
| М300 | 1:1,9:3,7 | 16:30 |
| М400 | 1:1,2:2,5 | 11:24 |
Таблица пропорций бетона на основе цемента марка М500
| Марка бетона | Массовые пропорции: цемента: песка: щебенки, кг | Объемные пропорции на 10 литров цемента: песок: щебень, литры |
| М100 | 1:5,8:8 | 53:70 |
| М200 | 1:3,4:5,5 | 32:49 |
| М300 | 1:2,3:4,2 | 22:37 |
| М400 | 1:1,5:3,1 | 14:28 |
Совет! В связи с тем, что масса конкретного цемента, песка и щебня могут существенно варьироваться в зависимости от конкретной плотности и влажности, перед тем как начать приготовление бетона следует выполнить расчет количества компонентов в килограммах.
Далее затарить (взвесить бытовым кантером или бытовыми весами) ведро или другую подходящую емкость наполненную цементом, песком и щебнем (как единицу измерения), и таким образом привести единицу измерения «килограммы» к единице измерения – «ведро/емкость». Теперь можно пользоваться ведром или емкостью для отмера компонентов бетона с учетом указанных выше соотношений.
Состав и пропорции бетона для фундамента
В этой статье мы рассмотрим с вами: что такое бетон, из чего он состоит, что такое марка бетона, в каких пропорциях в нем присутствуют компоненты и как сделать бетон для разных видов фундамента.
Состав бетона для фундамента
Думаем, большинство из вас и так уже знает, что такое бетон. Напомним, это раствор для возведения крепких каменных конструкций в строительстве. Его применяют для создания фундаментов, перекрытий, опор и столбов, плотин и дамб, дорог и отмосток вокруг зданий. Короче, сфера применения бетона очень обширна. Мы же рассмотрим с вами частный случай, а именно бетон для фундамента.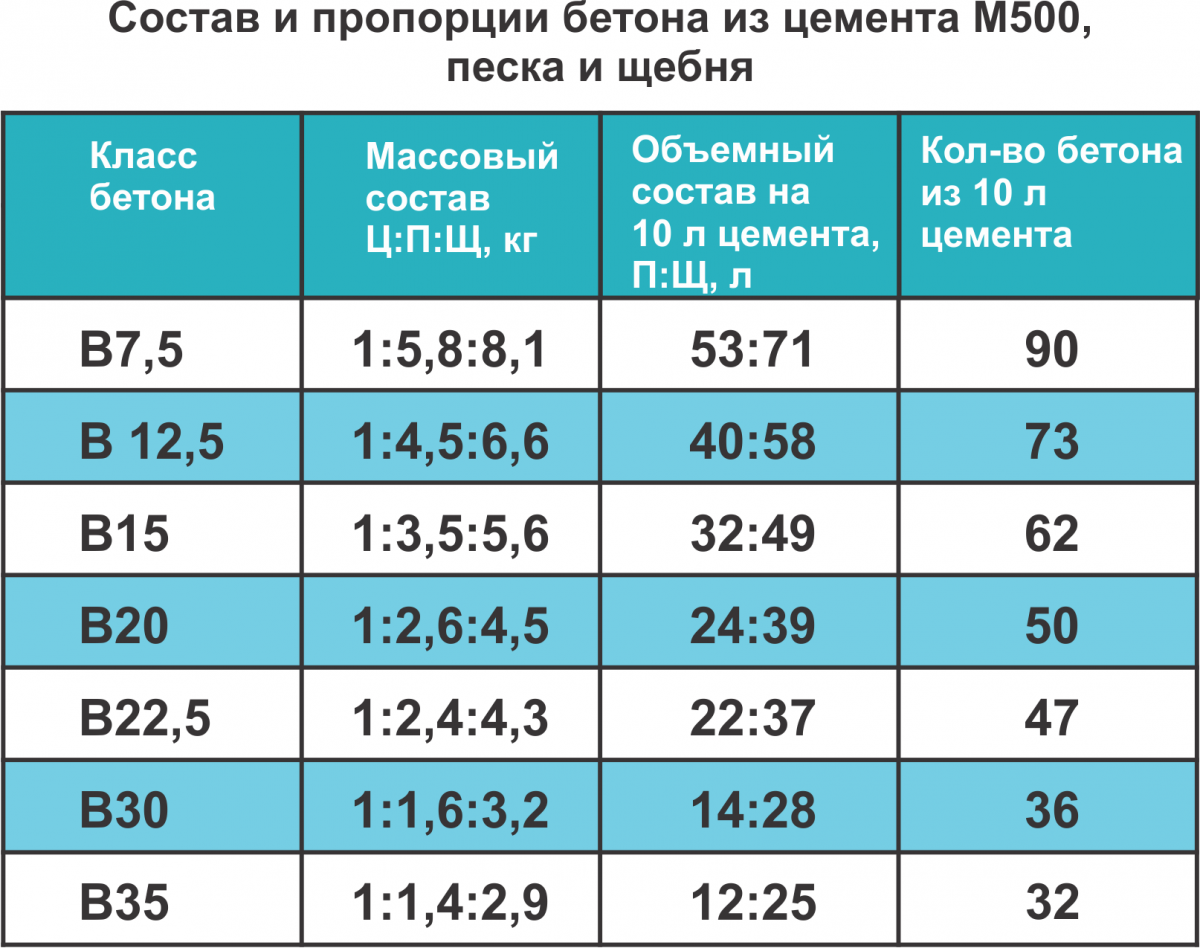
Для постройки фундамента зданий, хозяйственных построек, заборов и т.п. применяют бетон состоящий из:
- Цемент – главный компонент бетона для фундамента. Он является основным связующим наполнителем в бетоне.
- Песок – в бетоне для фундамента должен быть обязательно чистый, среднего размера карьерный или речной песок. Никаких примесей типа глины в нем не допускается.
- Щебень – для фундамента необходим гранитный или гравийный щебень фракции 5-20 мм.
- Вода – должна быть чистой.
- Пластификатор – в последнее время широко применяются различные пластификаторы для бетона. Если вы хотите сделать качественный бетон для фундамента, обязательно воспользуйтесь подходящим для ваших нужд пластификатором. Он существенно облегчит вам замес и применение бетона, очистку инструмента, увеличит время работы с бетоном, добавит ему прочности и пластичности. Также есть специальные добавки для работы на морозе, добавляющие бетону для фундамента гидроизолирующих свойств и другие.

Состав и пропорции бетона для фундамента определяют его марку. Что это такое? Читайте об этом дальше.
Марка бетона для фундамента
Сразу определимся с вами, что для постройки фундамента подойдет марка бетона М100 – М350. А теперь посмотрим, от чего она зависит и что это такое.
Все достаточно просто: буква М обозначает марку бетона и показывает в цифрах предел прочности. Т.е. сколько килограмм на квадратный сантиметр выдержит нагрузку бетон этой марки. Марка М200, самая распространенная для строительства фундаментов для частных домов, означает, что бетон выдержит нагрузку в 200 кг на см2.
Помимо марки бетона, зачастую используют такое понятие как класс бетона. Обозначается он буквой «В». Для фундамента подойдет бетон класса В7,5 – В25. Ниже смотрите таблицу соответствия класса и марки бетона.
Итак, какой марки или класс бетона подойдет для определенного вида фундамента?
Какой бетон нужен для фундамента
В зависимости от того, для какой постройки вы хотите возвести фундамент, нужно выбрать правильную марку бетона. Чем ответственней и тяжелей будет строение, тем крепче должен быть бетон для фундамента и тем выше должна быть марка или класс бетона.
Чем ответственней и тяжелей будет строение, тем крепче должен быть бетон для фундамента и тем выше должна быть марка или класс бетона.
Для постройки фундамента легких хозяйственных построек, таких как беседка, теплица, курятник, подойдет бетон М100-М150.
Для бани, гаража и т.п. можно использовать бетон М150-М200.
Для фундамента частного дома используйте бетон марки М200 и выше.
Все приведенные цифры весьма условны. И если у вас нет проекта возводимой конструкции, а вы сомневаетесь в достаточной прочности будущего фундамента, возьмите бетон классом повыше. Учитывайте также, что самостоятельно приготовленный бетон для фундамента, может отличаться маркой от заводского. И как правило, в меньшую сторону.
Пропорции бетона для фундамента
Итак, вы определились с маркой бетона для своего фундамента. Пора узнать, какие же пропорции бетона для фундамента надо соблюсти для этого.
Не секрет, что большинство «домашних строителей» пользуются стандартными формулами с пропорциями компонентов для приготовления бетона для фундамента.
В основном, пользуются двумя их видами:
- Для «обычного» бетона — 1 часть цемента, 3 части песка, 5 частей щебня. Воду добавляют по минимуму, но до пластичной консистенции.
- Для «крепкого» бетона – 1 часть цемента, 2 части песка, 4 щебня.
В принципе, такие формулы имеют право на жизнь, потому что подходят для большинства фундаментов в частной застройке. Если же вы хотите построить свой фундамент правильно, воспользуйтесь таблицей, которая подскажет пропорции бетона для фундамента.
В таблице приведены не только пропорции бетона для фундамента в килограммах, но и пропорции в частях. Так как многие строители используют для отмеривания нужных пропорций, к примеру, в ведрах или лопатах. Если вам удобнее использовать такой способ дозировки компонентов, то в таблице вы найдете пропорции бетона для фундамента в ведрах. Потому что «части» можно заменить любой мерой объема. Будь то ведра, лопаты, черпаки и даже руки.
Не забывайте, что пропорции бетона для фундамента в килограммах и ведрах, это не одно и то же. Потому как цемент, песок, щебень и вода имеют разный удельный вес. Ведро объемом 10 литров будет весить 10 кг с водой, около 12 кг с цементом, 14 кг с песком и 15 кг с щебнем. Но и эти цифры условны, т.к. цемент может быть как рыхлым, так и слежавшимся. Песок мокрым, а щебень крупным или мелким.
Потому как цемент, песок, щебень и вода имеют разный удельный вес. Ведро объемом 10 литров будет весить 10 кг с водой, около 12 кг с цементом, 14 кг с песком и 15 кг с щебнем. Но и эти цифры условны, т.к. цемент может быть как рыхлым, так и слежавшимся. Песок мокрым, а щебень крупным или мелким.
Совет! Для облегчения расчета состава бетона воспользуйтесь одним из наших бесплатных строительных калькуляторов онлайн.
И напоследок, посмотрите видео, в котором доступно поясняется как сделать и все пропорции бетона для фундамента. Удачи в постройке!
Правильный бетон по нормативам. Видео.
Пропорция
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений.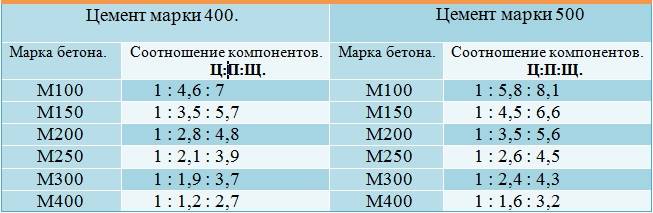 Например, отношение равно отношению
Например, отношение равно отношению
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:
Предположим, что в классе 10 девочек и 5 мальчиков
Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки
Теперь рассмотрим другой класс в котором две девочки и один мальчик
Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:
Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам
а также отношение 12 девочек к 2 мальчикам
Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение не пропорционально отношению .
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен.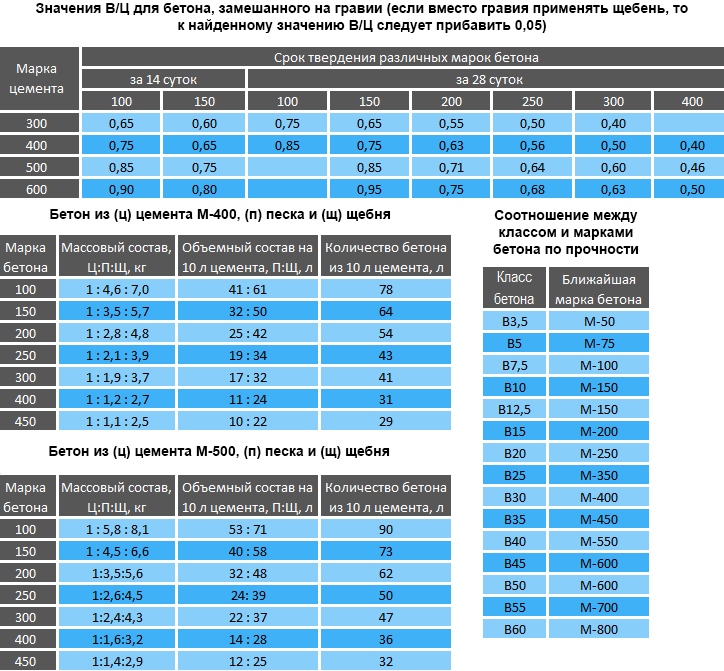 Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.
Поэтому в пропорции разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Как составить и рассчитать пропорцию: онлайн калькулятор
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 | ||||
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса.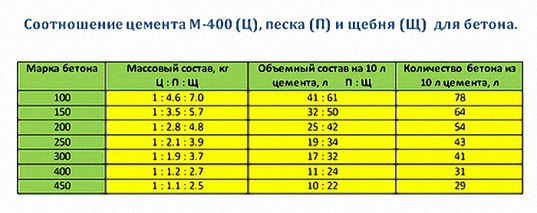 Сколько таблеток нужно выпить, если человек весит 70 кг?
Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Как развести бензин для бензопилы: официальный сайт Echotool.

Почему нужно смешивать масло и бензин
Для нормальной работы любому двигателю внутреннего сгорания нужны, как минимум, две вещи:
- Топливо — вернее топливовоздушная смесь, приготовленная карбюратором, попадает в камеру сгорания, воспламеняется, расширяется, и «толкает» поршень вниз, за счёт чего выполняется полезная работа.
- Смазка — необходима для уменьшения силы трения между соприкасающимися деталями двигателя.
В первую очередь, масло нужно для того, чтобы исключить так называемое «сухое» трение металла о металл. Из-за него контактирующие детали подвергаются критическому износу — появляются задиры, царапины, уменьшается компрессия, снижается ресурс. Также масло нужно для уплотнения зазоров.
Почему же нужно смешивать масло с топливом для бензопилы?
Это требование напрямую связано с особенностями устройства и принципом работы двухтактных двигателей, которыми оснащается данный инструмент.
Смазка деталей кривошипно-шатунного механизма и цилиндропоршневой группы здесь выполняется исключительно за счёт масла, находящегося в горючем. Благодаря особому устройству двигателя, топливовоздушная смесь попадает не только в камеру сгорания, но и в картер, где находится коленвал с шатуном. Таким образом, смазываются все трущиеся детали.
Соотношение количества масла и бензина для топливной смеси
Чтобы двухтактный двигатель бензопилы работал в оптимальном для него режиме, масло с бензином необходимо смешивать в определённых пропорциях. Они обычно указываются в инструкции к инструменту, а также на упаковках со смазкой. Рассмотрим вкратце, что будет, если рекомендуемых соотношений не соблюдать, или нарушать их по ошибке (незнанию).
Если масла добавить в бензин слишком мало, его концентрации не хватит для эффективной смазки трущихся деталей. Двигатель будет издавать звенящие звуки, чрезмерно греться, и быстро выйдет из строя. Много масла — тоже плохо, так как излишки не смогут полноценно сгорать. Это приведёт к образованию нагара на стенках цилиндра и поршне, загрязнению свечи зажигания, выхлопной системы. Также упадёт мощность, повысится расход топлива, и во время работы будет наблюдаться чрезмерная дымность выхлопа.
Много масла — тоже плохо, так как излишки не смогут полноценно сгорать. Это приведёт к образованию нагара на стенках цилиндра и поршне, загрязнению свечи зажигания, выхлопной системы. Также упадёт мощность, повысится расход топлива, и во время работы будет наблюдаться чрезмерная дымность выхлопа.
Чтобы этих проблем избежать, масло с бензином надо смешивать в рекомендуемых производителем пропорциях. Указываются они в виде соотношений — 1:50, 1:40, 1:25 и так далее. Любая из этих пропорций говорит о том, сколько масла нужно лить на объём топлива. Например, для приготовления смеси по пропорции 1:25 понадобится 1 литр масла на 25 литров бензина.
Важно не перепутать! Довольно часто указанные пропорции воспринимаются пользователями наоборот. К примеру, 1:50 понимается, как на 1 литр бензина 50 миллилитров масла. Это грубая ошибка, которая приведёт к повышенной концентрации масла в горючем. На самом деле при таком соотношении на 1 литр масла нужно всего 20 миллилитров масла.
Как не запутаться в пропорциях? Ведь мало кому надо готовить 50, или даже 25 литров топливной смеси для бензопилы. Тем более, что хранить смешанный с маслом бензин долго нельзя. Обычно готовят столько, сколько потребуется на день-два. А с учётом небольшого расхода бензопилы это 1-5 литров.
Есть три способа, как правильно развести бензин для бензопилы в небольших объёмах:
- Поделить 1000 на вторую цифру в пропорции. К примеру, нужно приготовить смесь в соотношении 1:40. Делите 1000 на 40, получаете 25. Столько миллилитров масла льёте на 1 литр бензина.
- Решить пропорцию, как в школе. Для этого требуемый объём бензина в литрах делим на вторую цифру в пропорции. В результате получаем нужный объём масла в литрах. Переводим литры в миллилитры для удобства. Допустим, вам нужно 3 литра смеси в пропорции 1:50. Решаем: 3/50=0,06 л. Чтобы превратить литры в миллилитры, переносим запятую на три знака вправо, и получаем 60 миллилитров.

- Посмотреть в таблице. Это самый простой, быстрый и наглядный способ, если пропорции стандартные. Остальные два способа нужны для того, чтобы понять, почему при пропорции 1:50 нужно лить на литр бензина 20 миллилитров масла, а не 50.
|
Пропорция |
Масла на 1 л бензина (мл) |
|
1:20 |
50 мл |
|
1:25 |
40 мл |
|
1:30 |
33 мл |
|
1:35 |
28 мл |
|
1:40 |
25 мл |
|
1:45 |
22 мл |
|
1:50 |
20 мл |
Теперь кратко о том, почему у разных производителей отличаются пропорции и нет какого-то единого стандарта. На это есть, как минимум, три причины. Во-первых, разные характеристики масел и бензина. Во-вторых, качество сборки двигателей (технологии, материалы) тоже отличается. В-третьих, режим эксплуатации инструмента. К примеру, для обкатки бензопил некоторых производителей рекомендуется добавлять в смесь на 20% больше масла.
На это есть, как минимум, три причины. Во-первых, разные характеристики масел и бензина. Во-вторых, качество сборки двигателей (технологии, материалы) тоже отличается. В-третьих, режим эксплуатации инструмента. К примеру, для обкатки бензопил некоторых производителей рекомендуется добавлять в смесь на 20% больше масла.
Пошаговая инструкция по заправке
Для приготовления топливной смеси и заправки бензопилы понадобится:
- мерная ёмкость;
- чистый бензин с октановым числом 92;
- специальное масло для двухтактных моторов с воздушным охлаждением;
- ёмкость для готовой смеси;
- воронка.
Для измерения объёмов можно использовать ёмкость, которыми обычно комплектуются бензиновые инструменты. Также можно купить специальные фирменные канистры с отделами и мерными приспособлениями.
Пошаговая инструкция:
- Приготовьте ёмкость для готовой топливной смеси.
 Её вместительности должно хватить и для бензина, и для масла.
Её вместительности должно хватить и для бензина, и для масла. - Посчитайте пропорцию смазки и бензина, исходя из руководства по эксплуатации, и воспользовавшись одним из способов выше.
- Отмерьте и налейте в ёмкость требуемый объём бензина.
- При помощи мерного стакана, штатной бутылочки или шприца отмерьте и добавьте в бензин нужный объём масла.
- Ёмкость для готовой смеси в итоге не должна быть полной под завязку.
- Надёжно закройте ёмкость крышкой, и несколько раз переверните её для того, чтобы масло смешалось с бензином.
- Заправьте приготовленную смесь в топливный бак бензопилы.
Вопреки гуляющему по Сети мнению, нет разницы, что первое заливать в ёмкость для приготовления смеси — бензин или масло. Главное, не забудьте тщательно перемешать. Вот чего на самом деле не стоит делать, так это готовить топливную смесь непосредственно в топливном баке бензопилы.
назад в блог
Какая пропорция цемента для фундамента оптимальна?
Для постройки частного дома, в частности при монтаже свайно-винтового фундамента оптимальным считается состав: на одну часть цемента четыре части щебенки (1/4). А в пропорции цемента и песка берется соотношение 1\3, то есть на 1 часть цемента (М 400) идет 3 части песка.
А в пропорции цемента и песка берется соотношение 1\3, то есть на 1 часть цемента (М 400) идет 3 части песка.
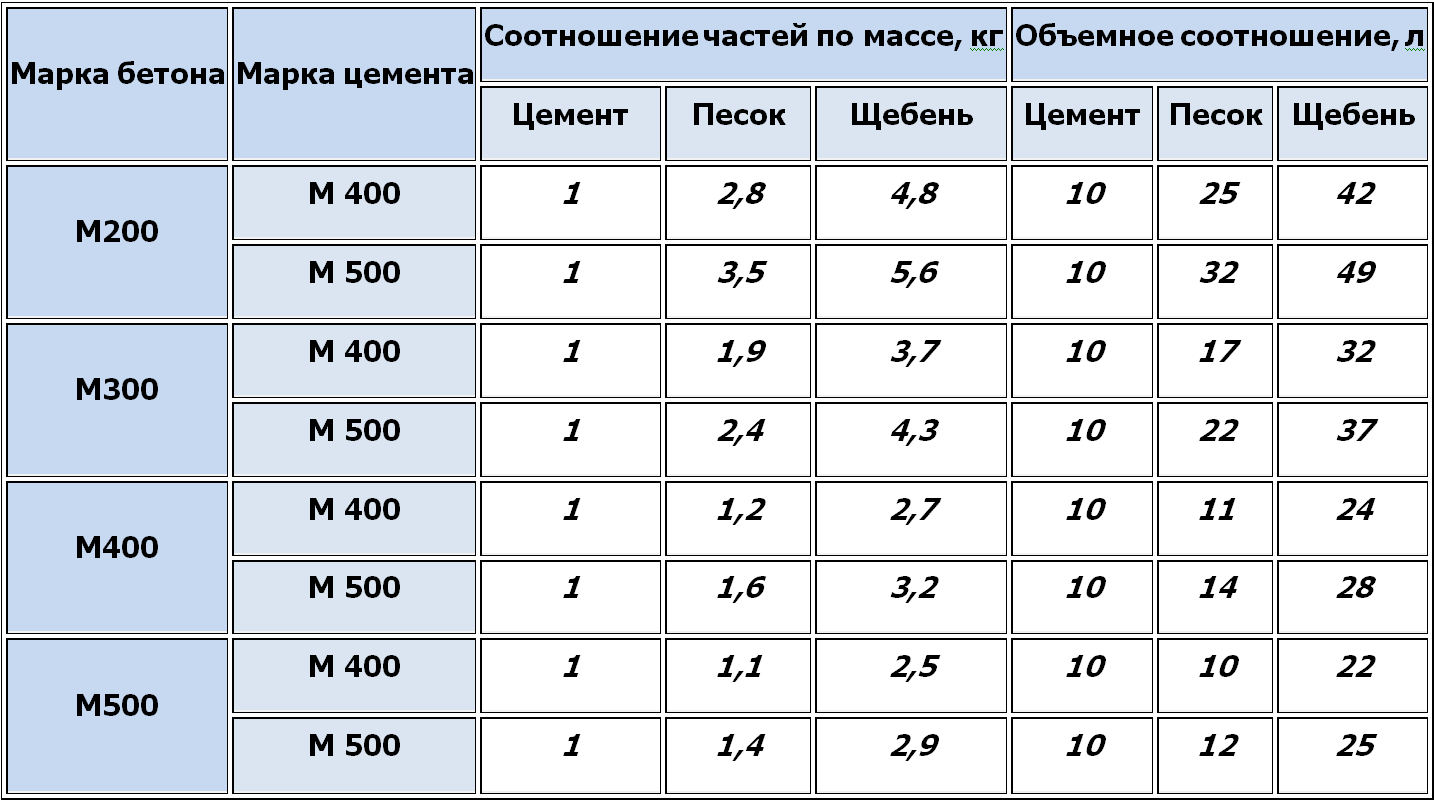
В таблице ниже приведены состав и пропорции бетона из цемента М-400 и М-500
Составляющие бетона для фундамента
Фундамент — основа любого здания, для постройки необходимо применять только высококачественный бетон, приготовленный с соблюдением необходимого соотношения исходных компонентов.
Бетон для фундамента готовят из трёх основных компонентов:
- Цемент. Основа бетона, придающая прочность. Этот сыпучий компонент выпускается нескольких марок, каждая под свои цели и нагрузки. Для фундамента стоит брать марку повышенной прочности.
- Песок и щебень. Наполнители бетона, который не позволяют развиваться усадкам и трещинам при застывании.
- Вода. Связывает цемент и наполнители в единое целое. От ее количества зависит время застывания смеси и набор фундаментом прочности.
К каждому компоненту строители применяют свои требования, соблюдение которых будет залогом получения качественного фундамента. Вода должна быть чистой, без примесей солей. Песок и щебень берут только нужной фракции, которые жёстко прописаны в СНИПах. Основной компонент – цемент – для возведения фундамента нужно брать не ниже марки М400, желательно М500, это позволит продлить срок службы фундамента.
Вода должна быть чистой, без примесей солей. Песок и щебень берут только нужной фракции, которые жёстко прописаны в СНИПах. Основной компонент – цемент – для возведения фундамента нужно брать не ниже марки М400, желательно М500, это позволит продлить срок службы фундамента.
Пропорции компонентов
Соотношений долей цемента и воды при заливке фундамента напрямую влияет на прочность, такое соотношение не должно превышать 3 к 4, иначе прочностные характеристики бетона в фундаменте не будут соответствовать требуемым значениям. Несущая способность фундамента будет невысока, а это его основная функция.
Вес цемента в цементном растворе должен составлять 1/4 от массы. В таблице ниже пример пропорций смеси на основе цемента «Мастер»
Непосредственно на строительной площадке редко взвешивают исходные компоненты — песок, цемент или воду. Это достаточно сложно сделать, строительные весы есть далеко не на каждой стройке. Строители чаще прибегают к замесу бетона с замером объёма компонентов. Для замеров используется ведро, оно есть на любой стройке.
Для замеров используется ведро, оно есть на любой стройке.
Для получения качественного бетона смешивают одно целое ведро цемента с заполненным не до краев ведром воды. Это соотношение могут чуть изменять, например, для заливки армированного фундамента. С толстой, мощной арматурой, раствор лучше приготовить чуть жиже, воды нужно соответственно немного больше. Такая смесь лучше проникает в опалубку, при этом не получается воздушных карманов. Если армирующего пояса при заливке бетона в опалубку не применялось, воды можно использовать меньше, это значительно ускоряет набор прочности цементом и снижает время его застывания.
При выполнении небольшого объёма работ, или когда работы производятся частями, бетон правильнее всего подготовить непосредственно на строительном объекте. Исходные компоненты смешивают прямо на площадке, вручную. Это достаточно медленно, зато позволяет четко контролировать соотношение сырья и его качество, что важно для получения качественного результата.
Для ускорения процесса замеса цемента часто применяют электрические мини-бетономешалки, В бетономешалки делается один замес раствора для фундамента в такой пропорции:
- 600 кг песка
- 1300 кг щебенки
- 300 кг цементна
Но у застройщика нет возможности взвешивать сыпучие материалы, когда он находится на месте строительства дома.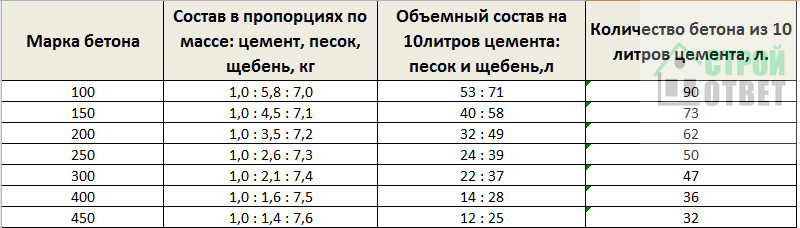 Возникает вопрос, какая пропорция цемента для фундамента оптимальна? Для этого нужно знать пропорции бетона для фундамента в ведрах. Поскольку у всех компонентов насыпная плотность примерно одинаковая можно перемерить их и тогда состав бетона для фундамента пропорции в ведрах будет примерно такой:
Возникает вопрос, какая пропорция цемента для фундамента оптимальна? Для этого нужно знать пропорции бетона для фундамента в ведрах. Поскольку у всех компонентов насыпная плотность примерно одинаковая можно перемерить их и тогда состав бетона для фундамента пропорции в ведрах будет примерно такой:
- Песок 2 ведра
- Щебенка 3.5 ведра
- Цемент 1 ведро
При определении количества воды ориентируются на меру цемента: на одно ведро цементного порошка нужно добавить не полное ведро воды. Объем, смотря по ситуации, может варьироваться. К примеру, если опалубка армирована, то бетон замешивается более пластичным, чтобы он легче проникал внутрь каркаса.
Без армирования практичнее сделать его жестким, это ускорит застывание. В обоих случаях воды нужно добавлять столько, чтобы в готовом растворе не было лужиц. Для получения одного куба бетона разных марок оптимальное соотношение компонентов в объемном выражении изложено в таблице:
Соотношение компонентов в объемном выражении
Для объемов заливки фундамента более 8 м3 стоит задуматься о покупке готового бетона в миксере. В таком случае цемент, песок и щебень будут замешаны на заводе, на стройку готовая смесь доставляется в промышленном миксере-бетономешалке. Это ускоряет процесс заливки фундамента, однако сложнее контролировать качество получаемого бетона, на данном рынке много мошенничества, когда в смесь на заводе кладут меньше цемента, заменяя его дешёвым песком и водой.
В таком случае цемент, песок и щебень будут замешаны на заводе, на стройку готовая смесь доставляется в промышленном миксере-бетономешалке. Это ускоряет процесс заливки фундамента, однако сложнее контролировать качество получаемого бетона, на данном рынке много мошенничества, когда в смесь на заводе кладут меньше цемента, заменяя его дешёвым песком и водой.
Какой бы способ заливки фундамента цементом не был выбран, основное о чём нужно помнить всегда — только соблюдение нужных пропорций и контроль качества исходных компонентов позволит получить необходимый результат.
Пропорция цемента и песка для штукатурки
Для приготовления штукатурной смеси используют различные компоненты, в основном приготавливается цементный раствор. Основными компонентами является цемент, песок, вода, также применяются различные добавки, которые оказывают функциональное влияние на смесь.
Какой цемент используют для штукатурки?
Обычно для приготовления штукатурного состава используют портландцементы не меньше 400 марки, иногда применяют 500 марку.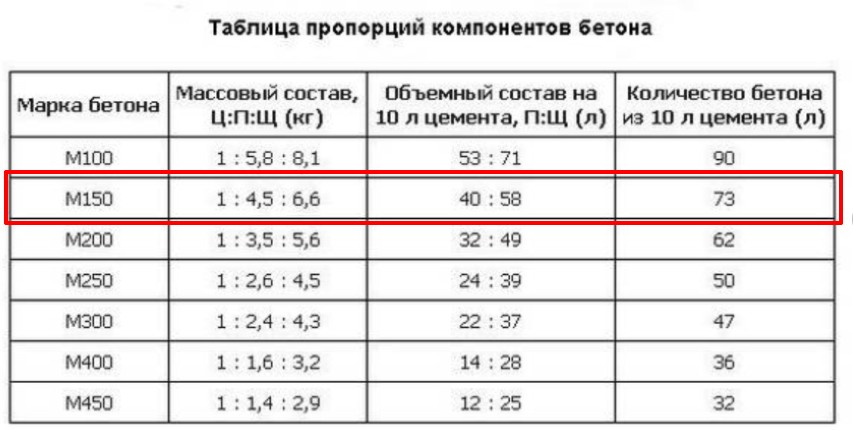 Многие имеют знания и опыт о пропорциях компонентов для раствора, но не всегда способны подобрать марку цемента для определенного вида штукатурной смеси.
Многие имеют знания и опыт о пропорциях компонентов для раствора, но не всегда способны подобрать марку цемента для определенного вида штукатурной смеси.
Чтобы выполнить работу на крупной площади, где маленькое количество исправлений, или для выравнивания поверхности стен, используют 400 марку первого типа, эти указания можно найти на упаковке. Хорошо подходит цемент для штукатурки внешних стен, он используется при повышенной влажности, и низкой температуры.
Второй вид цемента отличается специальными добавками, которые уменьшают внутреннее напряжение отливок из бетона и цемента, улучшают пластичность, и устойчивость к морозу. Таким видом цемента пользуются при выравнивании стен.
Использование различных добавок
Если штукатурный состав неправильно приготовлен, то его прилипание к бетонным или кирпичным поверхностям будет некачественным. При правильной консистенции, раствор будет сползать с мастерка за 8 секунд одной массой. Если смесь стекает или прочно прилипает к мастерку, то приготовление выполнено неправильно.
Чтобы повысить прилипание раствора, используют специальные добавки, корбоцеллюлозные или полиацетатные клеевые составы, они имеют порошкообразный вид, и растворяются в воде. Такие добавки способны вытеснять воздух с поверхности состава штукатурки.В результате оштукатуренная поверхность имеет гладкую, и ровную структуру.
Также для подготовки поверхности, и приготовления штукатурки используют составы КМС в жидком виде, их применяют для грунтовки стен, и добавляют в раствор.
Чтобы улучшить пластичность раствора на основе 400 цемента, используют обычный стиральный порошок или жидкое моющее средство на синтетической основе, на 50 литров состава добавляют 70 грамм.
Похожее действие оказывает жирная глина, на 15 литров воды добавляют 100 грамм. Её тщательно растирают в жидкости, а затем добавляют в смесь цемента с песком. При этом штукатурный состав высыхает дольше, чем обычный раствор. При слишком большом добавлении глины, после высыхания, поверхность может потрескаться.
Вместо глины можно использовать известковую пасту, такой раствор приготавливают для штукатурки внешних стен или подвальных помещений.
Если поверхность подвержена изменению температуры, то нужно воспользоваться добавкой из рубленного волоконного материала, в основе которого лежит полимер – стекловолокно.
Особые составляющие для штукатурного состава
Чтобы уменьшить плотность штукатурного слоя, и увеличить теплоизоляционные свойства, в штукатурную смесь добавляют специальный песок или природное сырье в молотом виде. Крупа или измельченный в муку доломит, вермикулит, способны увеличить поры, и микрополости в цементном растворе на 30 процентов.
Такие компоненты добавляются в пропорциях до 27 процентов, при этом потеря тепла сокращается, и улучшаются звукоизоляционные качества, также сохраняется водоотталкивающая функция.
Пропорция цемента и песка для штукатурки
Отделка кирпичных построек штукатуркой является обязательным процессом, для этого используют раствор на основе цемента и песка, существует состав, в который добавляют известь. При приготовлении обычного раствора берут одну часть цемента, и 5 песка. Воду наливают до соблюдения необходимой консистенции.
При приготовлении обычного раствора берут одну часть цемента, и 5 песка. Воду наливают до соблюдения необходимой консистенции.
Пропорции песка и цемента зависят от того какой вид штукатурки будет наноситься. Чтобы выполнить набрызг, приготавливают жирные составы, соблюдая пропорции 1 к 3, а для накрывочных слоев, используют прочную смесь 1 к 2 или 1 к 1.
Пропорция составляющих зависит от среды применения, для внутренних поверхностей в сухих, и теплых помещениях берут 1 часть цемента, и 4 или 5 песка. Чтобы оштукатурить внешние стены, раствор приготавливают из 3 частей песка, и 1 цемента 400 марки.
Если толщина штукатурного слоя от 2 сантиметров, то на один квадратный метр уходит до 6 килограмм цемента, и 20 песка, при пропорциях 1 к 4.
Составы для штукатурки на цементной основе
Составы на цементной основе используются для отделки поверхностей, которые оказываются под воздействием влажности, независимо внутри или снаружи помещения.
- Раствор цементного вида приготавливают, соблюдая пропорции 1 к 3 или 1 к 4, это зависит от целей использования.
 Компоненты разбавляют водой, и тщательно перемешивают, чтобы получить однородную массу. Весь состав необходимо израсходовать в течении одного часа, иначе он потеряет своё качество.
Компоненты разбавляют водой, и тщательно перемешивают, чтобы получить однородную массу. Весь состав необходимо израсходовать в течении одного часа, иначе он потеряет своё качество. - Для приготовления цементного раствора с известью, смешивают одну часть портландцемента с 0,5 частью известкового теста, и 2 части промытого песка. Такой состав изготавливается двумя способами:
- вначале смешивается известковое тесто с песком, затем добавляют цемент, воду, и перемешивают до необходимой консистенции;
- выполняют раствор из цемента и песка, хорошо размешивают, добавляя известковое молоко.
Разновидности штукатурных составов
Чтобы выполнить отделку стен штукатуркой, её необходимо приготовить, для этого используют наполнитель, и вяжущий материал, в качестве которого добавляют цемент, известь или глину. Наполнителем служит песок, если его не добавить, то состав потеряет прочность, а поверхность потрескается. Растворы могут быть разных видов.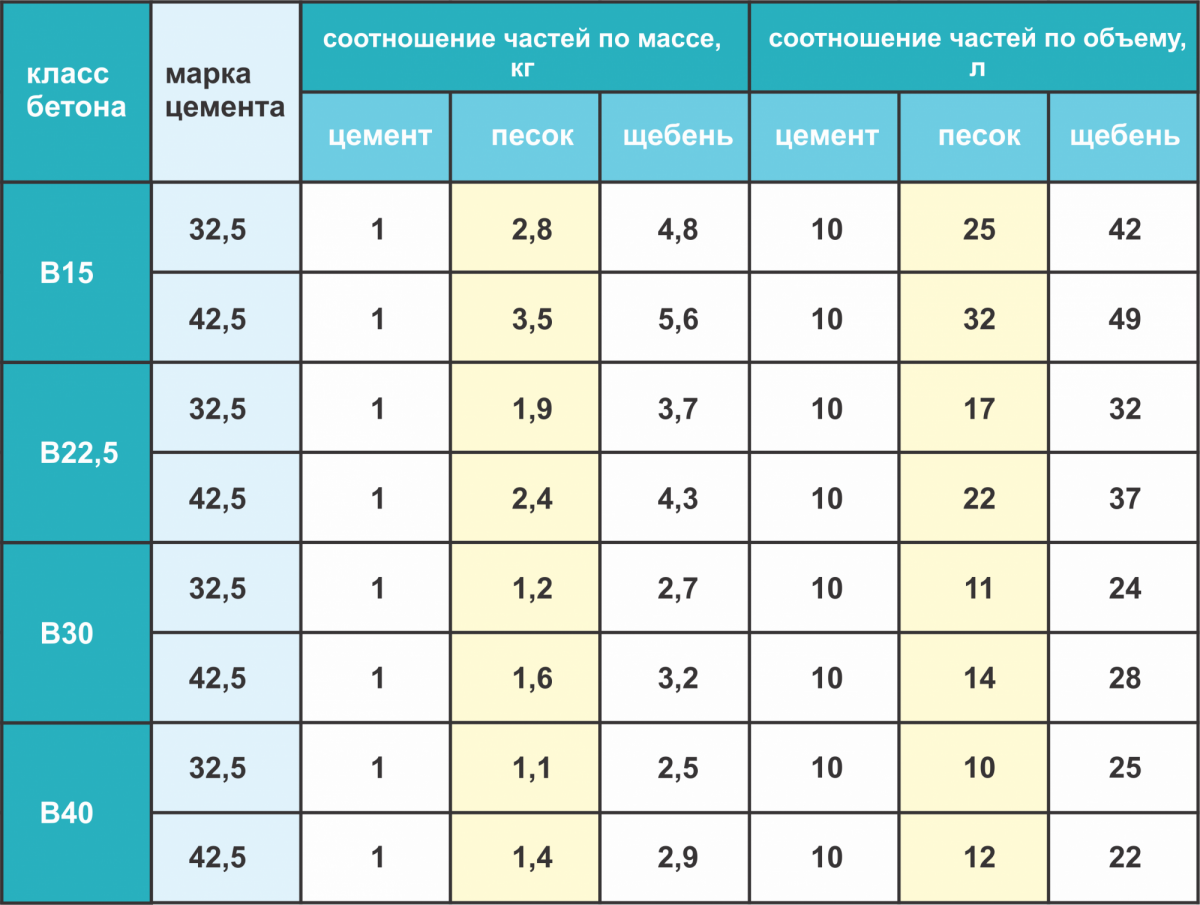
- Раствор на основе цемента или с добавлением извести, его применяют для отделки внешних поверхностей, которые подвергаются постоянной влажности. Для обработки внутренних помещений с такой же проблемой, например ванной комнаты.
- Известковый или с добавлением гипса, и глины, применяют для наружных, и внутренних работ, при этом поверхность не должна подвергаться влажности.
- Состав на основе глины и цемента используется для внутренних и наружных работ, поверхности которых имеют умеренную влажность.
Особенности состава для штукатурки
Чтобы приготовить состав высокого качества, все сухие материалы просеивают через специальное сито. Раствор готов к выполнению работы в том случае, если он имеет однородную массу, нужную жирность, и хорошо удерживается на поверхности, не дает трещины после высыхания.
Растворы могут быть тощими или иметь повышенную, и нормальную жирность. Жирные составы включают в себя большое содержание вяжущего вещества, в результате на оштукатуренной поверхности появляются трещины. При нормальном составе, все компоненты добавляются в правильной пропорции. Тощие смеси имеют большое количество наполнителя, при этом штукатурный слой теряет прочность, но покрытие не дает усадку, и трещин.
При нормальном составе, все компоненты добавляются в правильной пропорции. Тощие смеси имеют большое количество наполнителя, при этом штукатурный слой теряет прочность, но покрытие не дает усадку, и трещин.
Определяют жирность предметом, которым перемешивается раствор. Если смесь сильно прилипает, то она имеет жирный состав, необходимо добавление наполнителя, то есть песка. При отсутствии прилипания, состав считается тощим, поэтому нужно добавить вяжущий материал. Раствор считается приемлемым для работы, если прилипание имеет среднюю степень.
Современные материалы для штукатурки
На современном рынке большое разнообразие сухих смесей для штукатурных работ, их основой является портландцемент. Такие смеси содержат полимерные добавки, которые увеличивают пластичность раствора, и способствуют его качественному прилипанию к поверхности. Прочность штукатурки увеличивается в разы, смесь отличается рядом преимуществ.
- При выполнении работ, не используют штукатурную сетку, что позволяет сэкономить расход раствора.

- Раствор становиться эластичным, хорошо переносит изменения температуры, и повышенную влажность.
- Оштукатуренные поверхности пропускают воздух, при этом не крошатся от попадания влажности.
Приготовление растворов из таких смесей не составляет труда, необходимо просто добавить нужное количество воды. Современные составы позволяют выполнять тонкослойную работу, раствор приготавливают в необходимом количестве, это сокращает расходы, и создает удобство в использовании.
При изготовлении раствора, учитывают тип обрабатываемой поверхности, и условия, в которых она находится. Чтобы изготовить раствор для штукатурки, используют ингредиенты, имеющие высокое качество, это оказывает влияние на качество смеси, и долговечности отделки.
Стандартным составом считается цементно-песчаный раствор, который используют для оштукатуривания различных поверхностей, его применяют для отделки, и выравнивания внутренних, и внешних стен. В состав штукатурки входит три основные компонента.
- Чтобы приготовить штукатурный состав, берут портландцемент марки 200-500. Штукатурка не является требовательной к особой прочности, поэтому для отделки внутренних стен, можно взять 200 марку. Чтобы обработать внешние поверхности, используют 400 или 500 марку, такой вид цемента применяется для всех помещений с высокой влажностью.
- Песок должен быть очищенным. Для штукатурки можно использовать любой песок, для лучшего результата применяют карьерный вид, который имеет фракцию от 20 до 40. Нельзя использовать вещество с примесью ила, грязи или глины, песок должен быть просеянным, мелкая фракция не подойдет для такого раствора.
- Вода может добавляться любая, техническая, речная или водопроводная. Её добавляют в таком количестве, чтобы получить нужную консистенцию раствора.
При использовании натуральных природных компонентов, и правильном составе, после высыхания, раствор застывает, и образуется ровное покрытие с высокой прочностью, которое имеет долгий срок службы. Материал является устойчивым к влажности, морозам, и различным агрессивным веществам, поэтому его используют для отделки внешних и внутренних стен, подвалов или подсобных зданий, которые не отапливаются.
Раствор можно приготовить самостоятельно, это не требует особенных знаний, и опыта, главное, соблюдать пропорции основных компонентов, можно применять специальные добавки, которые увеличивают качество состава. Также нужно учитывать, что приобрести смесь в готовом виде оказывается дороже, чем сделать её самому, то есть при самостоятельном изготовлении, можно экономить на расходах.
Если все пропорции соблюдены правильно, то оштукатуренная поверхность будет прочной, покрытие не даст усадку или трещин, такая отделка является долговечной, устойчивой к изменениям температуры, и влажности. Перед тем как приступить к работе, раствор проверяют на жирность, это является обязательным условием.
Определение пропорции по Merriam-Webster
доля
| \ prə-ˈpȯr-shən
\
1
: гармоничное отношение частей друг к другу или ко всему : баланс, симметрия
2а
: собственных или равных долей
каждый выполнил свою долю работы
3
: отношение одной части к другой или к целому по величине, количеству или степени : отношение
5
: заявление о равенстве между двумя отношениями, в котором первое из четырех членов, разделенное на второе, равно третьему, разделенному на четвертое (как в случае 4/2 = 10/5) — сравните крайнее значение 1b, среднее значение 1c
пропорциональный; дозирование \
прə- ˈpȯr- sh (ə-) niŋ
\
переходный глагол
1
: для регулировки размера (части или предмета) по сравнению с другими частями или предметами.
2
: , чтобы детали были гармоничными или симметричными.
Что такое пропорции | Типы | Примеры
Пропорция объясняется главным образом на основе соотношения и дробей.Дробь, представленная в виде a / b, в то время как соотношение a: b, тогда пропорция указывает, что два отношения равны. Здесь a и b — любые два целых числа. Соотношение и пропорция являются ключевыми основами для понимания различных концепций как в математике, так и в естествознании.
Пропорция находит применение при решении многих повседневных жизненных проблем, например, в бизнесе, при совершении транзакций или во время приготовления пищи и т. Д. Она устанавливает связь между двумя или более величинами и, таким образом, помогает в их сравнении.
Что такое пропорция?
Доля, как правило, определяется как часть, доля или количество, рассматриваемые в сравнительном отношении к целому. Определение пропорции гласит, что когда два отношения эквивалентны, они пропорциональны. Это уравнение или утверждение, используемое для обозначения равенства двух соотношений или дробей.
Пропорция — Определение
Пропорция — это математическое сравнение двух чисел. Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же соотношении, то говорят, что эти отношения прямо пропорциональны друг другу.Пропорции обозначаются символом «::» или «=».
Пропорция — Пример
Два соотношения считаются пропорциональными, если два соотношения равны. Например, время, затрачиваемое поездом на преодоление 50 км в час, равно времени, затраченному им на преодоление расстояния 250 км за 5 часов. Например, 50 км / час = 250 км / 5 часов.
Продолжение пропорций
Говорят, что любые три величины находятся в непрерывной пропорции, если соотношение между первым и вторым равно соотношению между вторым и третьим.Точно так же четыре количества в непрерывной пропорции будут иметь соотношение между первым и вторым, равное отношению между третьим и четвертым.
Например, рассмотрим два соотношения: a: b и c: d. Чтобы найти непрерывную пропорцию для двух заданных членов отношения, мы преобразуем их средние в один член / число. В общем случае это будет НОК средних, и для данного отношения НОК b и c будет bc. Таким образом, умножив первое отношение на c, а второе отношение на b, получим
- Первое соотношение- ca: bc
- Второе передаточное число- bc: bd
Таким образом, непрерывную пропорцию для данных соотношений можно записать в виде ca: bc: bd.
Соотношения и пропорции
Соотношение — это способ сравнения двух одинаковых количеств с помощью деления. Формула отношения для двух чисел a и b задается как a: b или a / b. Умножение и деление каждого члена отношения на одно и то же число (отличное от нуля) не влияет на соотношение.
Когда два или более таких отношения равны, говорят, что они находятся в соотношении .
Четвертый, третий и средний пропорциональный
Если a: b = c: d, то:
- d называется четвертым, пропорциональным a, b, c.
- c называется третьим, пропорциональным a и b.
- Среднее значение, пропорциональное между a и b, равно √ (ab).
Советы и рекомендации по пропорции
- a / b = c / d ⇒ ad = bc
- a / b = c / d ⇒ b / a = d / c
- a / b = c / d ⇒ a / c = b / d
- a / b = c / d ⇒ (a + b) / b = (c + d) / d
- a / b = c / d ⇒ (a — b / b = (c — d) / d
- a / (b + c) = b / (c + a) = c / (a + b) и a + b + c ≠ 0, тогда a = b = c.
- a / b = c / d ⇒ (a + b) / (a - b) = (c + d) / (c — d), которое известно как правило componendo -dividendo
- Если оба числа a и b умножаются или делятся на одно и то же число в соотношении a: b, то полученное соотношение остается таким же, как исходное соотношение.
Формула пропорции с примерами
Формула пропорции — это уравнение, которое можно решить для получения сравнительных значений. Для решения задач пропорций мы используем концепцию, согласно которой пропорция — это два равных друг другу соотношения. Мы имеем в виду это в смысле равенства двух дробей.
Формула соотношения
Предположим, что у нас есть любые две величины (или две сущности), и мы должны найти соотношение этих двух, тогда формула для отношения определяется как a: b ⇒ a / b , где
- a и b могут быть любыми двумя величинами.
- «а» называется первым членом или антецедентом .
- «b» называется вторым членом или последующим .
Например, в соотношении 5: 9 представляется как 5/9, где 5 является антецедентом, а 9 — следствием. 5: 9 = 10:18 = 15:27
Формула пропорции
Теперь предположим, что два соотношения пропорционально a: b и c: d. Два термина «b» и «c» называются «средствами или средними терминами», тогда как термины «a» и «d» известны как «крайние или крайние термины».’
a / b = c / d или a: b :: c: d. Например, давайте рассмотрим другой пример количества студентов в классе. Наше первое соотношение количества девочек и мальчиков составляет 2: 5, а соотношение остальных — 4: 8, тогда соотношение может быть записано как: 2: 5 :: 4: 8 или 2/5 = 4/8 Здесь 2 и 8 — крайности, а 5 и 4 — средние.
В зависимости от типа взаимосвязи, которую разделяют два или более количества, пропорция может быть классифицирована по различным типам. Есть два типа пропорций.
- Прямая пропорция
- Обратная пропорция
Прямая пропорция
Этот тип описывает прямую связь между двумя величинами. Проще говоря, если одно количество увеличивается, другое количество также увеличивается, и наоборот. Например, если скорость автомобиля увеличивается, он преодолевает большее расстояние за фиксированный промежуток времени. В обозначениях прямая пропорция записывается как y ∝ x.
Обратная пропорция
Этот тип описывает косвенную связь между двумя величинами.Проще говоря, если одно количество увеличивается, другое количество уменьшается, и наоборот. В обозначениях обратная пропорция записывается как y ∝ 1 / x. Например, увеличение скорости автомобиля позволит преодолеть фиксированное расстояние за меньшее время.
Важные примечания
- Пропорция — это математическое сравнение двух чисел.
- Основные пропорции бывают двух типов: прямые пропорции и обратные пропорции.
- Мы можем применить концепции пропорций к географии, сравнивая величины в физике, диетологии, кулинарии и т. Д.
- Пропорция — это математическое сравнение двух чисел.
- Мы можем применить концепции пропорций к географии, сравнивая величины в физике, диетологии, кулинарии и т. Д.
Свойства пропорции
Пропорция устанавливает эквивалентное соотношение между двумя соотношениями. Свойства пропорции, которой следует это соотношение:
- Дополнение — Если a: b = c: d, то a + c: b + d
- Вычитание — Если a: b = c: d, то a — c: b — d
- Дивидендо — Если a: b = c: d, то a — b: b = c — d: d
- Componendo — Если a: b = c: d, то a + b: b = c + d: d
- Alternendo — Если a: b = c: d, то a: c = b: d
- Invertendo — Если a: b = c: d, то b: a = d: c
- Компонент и дивидендо — Если a: b = c: d, то a + b: a — b = c + d: c — d
Разница между соотношением и пропорциями
Соотношение и пропорция — тесно связанные понятия.Пропорция означает равное соотношение между двумя или более соотношениями. Чтобы понять концепцию соотношения и пропорции, просмотрите разницу между соотношением и пропорцией, указанную здесь.
| С. № | Коэффициент | Пропорция |
| 1 | Отношение используется для сравнения размера двух вещей с одной и той же единицей измерения. | Пропорция используется для выражения отношения двух соотношений. |
| 2 | Это выражается двоеточием (:) или косой чертой (/). | Это выражается двойным двоеточием (: 🙂 или равным символу (=) |
| 3 | Это выражение. | Это уравнение. |
| 4 | Ключевое слово для различения соотношения в проблеме — «к каждому». | Ключевое слово для различения пропорций в задаче — «вне». |
Пропорции Связанные темы
Ниже приводится список тем, которые тесно связаны с Пропорцией в коммерческой математике.Эти темы также дадут вам представление о том, как такие концепции рассматриваются в Cuemath.
Часто задаваемые вопросы о пропорциях
Что вы имеете в виду под коэффициентом?
Отношение — это математическое выражение, записанное в форме a: b, которое выражает часть формы a / b, где a и b — любые целые числа. Например, дробь 1/3 может быть выражена как 1: 3 в форме отношения.
Что такое пропорция в математике?
Пропорция — это математическое сравнение двух чисел. Согласно пропорции, если два набора заданных чисел увеличиваются или уменьшаются в одном и том же соотношении, то говорят, что эти отношения прямо пропорциональны друг другу. Пропорции обозначаются символом «::» или «=». Например, 2: 5 :: 4: 8 или 2/5 = 4/8. Здесь 2 и 8 — крайности, а 5 и 4 — средние.
Как соотношение и пропорции используются в повседневной жизни?
Пропорции и пропорции используются ежедневно.Соотношения и пропорции используются в деловых операциях при работе с деньгами, сравнении количества по цене при совершении покупок и т. Д. Например, у предприятия может быть соотношение суммы прибыли, полученной от продажи определенного продукта, например 5 долларов США: 1, где говорится, что бизнес получает 2,50 доллара с каждой продажи.
Как узнать, составляют ли два соотношения пропорцию?
Если два отношения эквивалентны друг другу, то говорят, что они пропорциональны. Например, соотношения 1: 2, 2: 4 и 3: 6 являются эквивалентными соотношениями.
Как рассчитать пропорцию?
Пропорция рассчитывается по формуле пропорции, которая гласит: a: b :: c: d или a: b = c: d. Мы читаем это так, как «а» относится к «б», как «с» относится к «г».
Что такое разные типы пропорций?
В зависимости от типа взаимосвязи, которую разделяют два или более количества, пропорция может быть классифицирована по различным типам. Есть два типа пропорций.
- Прямая пропорция — описывает прямую взаимосвязь между двумя величинами.Проще говоря, если одно количество увеличивается, другое количество также увеличивается, и наоборот.
- Обратная пропорция — описывает косвенную связь между двумя величинами. Проще говоря, если одно количество увеличивается, другое количество уменьшается, и наоборот.
Каковы различные свойства пропорции?
Пропорция устанавливает эквивалентное соотношение между двумя соотношениями. Свойства пропорции, которой следует это соотношение:
- Дополнение — Если a: b = c: d, то a + c: b + d
- Вычитание — Если a: b = c: d, то a — c: b — d
- Дивидендо — Если a: b = c: d, то a — b: b = c — d: d
- Componendo — Если a: b = c: d, то a + b: b = c + d: d
- Alternendo — Если a: b = c: d, то a: c = b: d
- Invertendo — Если a: b = c: d, то b: a = d: c
- Компонент и дивидендо — Если a: b = c: d, то a + b: a — b = c + d: c — d
Соотношения и пропорции — Пропорции
Пропорция
просто утверждение, что два соотношения равны.Это можно записать двумя
способами: как две равные дроби a / b = c / d; или используя двоеточие, a: b = c: d. Следующие
пропорция читается как «двадцать равно двадцати пяти, как четыре — пяти».
В проблемах
включая пропорции, мы можем использовать перекрестные произведения, чтобы проверить,
равны и образуют пропорцию. Чтобы найти перекрестные произведения пропорции,
мы умножаем внешние члены, называемые крайними, и средние, называемые
значение.
Здесь 20 и
5 — крайности, а 25 и 4 — средние. Поскольку кросс-продукты
оба равны сотне, мы знаем, что эти отношения равны и что это
это верная пропорция.
Мы также можем
используйте перекрестные произведения, чтобы найти пропущенный член в пропорции. Вот пример.
В фильме ужасов с участием гигантского жука он выглядел на 50 футов выше.
длинный. Однако для жука использовалась модель, которая на самом деле была всего 20 дюймов.
длинный.В фильме также использовалась модель здания высотой 30 дюймов. Какого роста
здание кажется в фильме?
Сначала напишите
пропорция, в которой пропущенный член заменяется буквой. Мы находим
произведите перекрестные произведения, умножив 20 на x и 50 на 30. Затем разделите на
найти х. Внимательно изучите этот шаг, потому что это метод, который мы будем часто использовать.
по алгебре. Мы пытаемся найти неизвестное нам число x в левой части
уравнение само по себе.Поскольку x умножается на 20, мы можем использовать «обратный»
умножения, то есть деления, чтобы избавиться от 20. Мы можем разделить и то, и другое.
стороны уравнения на одно и то же число, не меняя смысла
уравнение. Когда мы разделим обе стороны на 20, мы обнаружим, что здание будет
кажутся 75 футов высотой.
Обратите внимание, что мы
используя обратное умножение на 20, то есть деление на 20, чтобы получить только x
на одной стороне.
назад
наверх
Что такое пропорция в математике? — Определение и практические проблемы — Видео и стенограмма урока
Пропорции и эквивалентные дроби
Вы можете определить, пропорциональны ли две дроби, используя перекрестное умножение. Пропорциональны только эквивалентные дроби.
Для этого умножьте знаменатель, нижнее число дроби, первой дроби на числитель, верхнее число дроби.Проделайте то же самое с числителем первой дроби и знаменателем второй дроби. Если произведения двух уравнений одинаковы, то у вас есть эквивалентные дроби, и они пропорциональны!
Другой пример:
Эквивалентны и пропорциональны ли следующие дроби?
A. 4/5 = 8/10
Да, дроби эквивалентны и пропорциональны. Когда мы завершим перекрестное умножение, мы увидим, что 4 * 10 = 40 и 5 * 8 = 40.
B. 2/3 = 9/12
Нет, дроби не эквивалентны и не пропорциональны. Это потому, что, когда мы завершаем перекрестное умножение, мы видим, что 2 * 12 = 24 и 3 * 9 = 27. Поскольку эти два произведения не совпадают, эти дроби не эквивалентны и не пропорциональны.
Резюме урока
В заключение, пропорция представляет собой сравнение чисел. Пропорции часто записываются двумя числами, разделенными двоеточием. Пропорции также можно записать в виде двух эквивалентных дробей.Вы можете проверить две дроби, чтобы убедиться, что они пропорциональны и эквивалентны, перемножив числители и знаменатели двух дробей. Если вы получите такое же число, значит, ваши дроби эквивалентны.
Примечания к пропорциям
- Пропорции часто обозначаются словами «одна из …»
- Пропорции могут быть записаны как дроби или с двоеточием
- Пропорциональны только эквивалентные дроби
Результаты обучения
После того, как вы закончите, вы должны быть в состоянии:
- Вспомнить, какова пропорция
- Напишите пропорцию
- Проверить, пропорциональна ли пара дробей
Пропорции в математике — Практическое упражнение:
Следующее практическое упражнение предназначено для студентов, чтобы они могли применить свои знания о пропорции в математике и понять ее полезность в реальной жизни.
Корпус:
У вас и вашей семьи есть кукольный магазин в Иллинойсе. В течение многих лет вы создавали одну куклу — Дарди. Дарди всегда был культовой куклой, в которую играли сотни детей в вашем районе. Каждый Дарди создается вручную вами и членами вашей семьи исключительно хорошо. Однако в прошлом году ваша семья решила, что Дарди пора обзавестись собакой в качестве компаньона: так был создан Барки — собачья кукла. Вашей семье интересно узнать, насколько хорошо продается кукла Барки по сравнению с общим объемом продаж кукол.Данные о продажах представлены ниже.
| Год | Прошлый год | В этом году |
|---|---|---|
| Barky Sales | 60 | 95 |
| Dardie Sales | 140 | 190 |
Требуется:
Вычислите следующие пропорции на основе предоставленных данных о продажах:
- Доля продаж Барки относительно общего объема продаж в этом году (укажите в своем ответе наименьшую возможную долю).
- Доля продаж Барки относительно общего объема продаж за прошлый год (ответьте как минимально возможную долю).
- Доля продаж Barky увеличилась, уменьшилась или осталась неизменной из года в год?
Решение:
1.
= Продажи Барки в этом году / Общие продажи в этом году
= 95/285
= 1/3
2.
= Продажи Барки в прошлом году / Общий объем продаж в прошлом году
= 60/200
= 3/10
3.
Давайте перенесем ответ в # 1 выше в том же знаменателе # 2.
1/3 и 3/10
(1 * 3,3) / (3 * 3,3) против 3/10
3.3 / 10 и 3/10
Ответ состоит в том, что соотношение увеличилось на на , поскольку 3,3 / 10 больше, чем 3/10.
Пропорции — Объяснение и примеры
Трудно представить, какой была бы наша жизнь без математических понятий, таких как пропорции. В нашей повседневной жизни мы часто сталкиваемся с пропорциями и соотношениями, когда идем за покупками, готовим, в поездке по профессии и т. Д.
Соотношения и пропорции необходимы для — эффективной работы. В этой статье мы узнаем, как рассчитать пропорции и применить полученные знания для решения типовых задач, но перед этим давайте начнем с определения соотношений.
Отношение — это способ сравнения двух или более величин. Знак, используемый для обозначения отношения, — двоеточие «: » . Предположим, что a и b — две разные величины или числа, тогда отношение a к b можно записать как a / b или a: b.Точно так же отношение b к a также может быть представлено как b: a или b / a. Первая величина в соотношении называется антецедентом, а вторая величина — как следствие.
Примеры соотношений: : или 3: 4, 1/5 или 1: 5, 199/389 или 199: 389 и т. Д. Из этого примера очевидно, что соотношение — это просто дробь, в которой антецедент представляет собой числитель, а консеквент — знаменатель.
Знаменитый рисунок Леонардо да Винчи «Витрувианский человек» был основан на идеальном соотношении человеческого тела.Каждая часть тела занимает разное соотношение, например, лицо занимает около 1/10 от общей высоты, а голова занимает около 1/8 от общей высоты. Писатели средневековья впервые использовали слово proportio (пропорция). В 1948 году Ле Корбюзье дал систему пропорций.
Что такое пропорция?
Пропорция — это выражение, которое говорит нам, что два соотношения эквивалентны. Два отношения называются пропорциональными, если они эквивалентны. Пропорции обозначаются знаком «:» или «=».Например, если a, b, c и d — целые числа, тогда пропорция записывается как a: b = c: d или a / b = c / d или b: a = d: c. Например, отношения 3: 5 и 15:25 пропорциональны и записываются как 3: 5 = 15: 25
Четыре числа a, b, c и d известны как члены пропорции. Первый a и последний член d называются крайними членами, а второй и третий члены в пропорциональном выражении называются средними членами.
Как решить пропорции?
Легко вычислить, пропорциональны ли соотношения.Чтобы проверить, пропорционально ли соотношение a: b и c: d.
- Умножьте первый член на последний член: a x d
- Умножьте второй член на третий член: b x c
- Если произведение крайних членов равно произведению средних значений, то отношения пропорциональны: a x d = b x c
Непрерывная пропорция
Говорят, что два отношения a: b и b: c находятся в непрерывной пропорции, если a: b = b: c. В этом случае член c называется третьей пропорцией a и b, тогда как b называется средней пропорцией между членами a и c.
Когда члены a, b и c находятся в непрерывной пропорции, получается следующая формула:
а / б = б / с
Перекрестное умножение членов дает; a x c = b x b, следовательно,
b² = ac
Пример 1
Узнайте, пропорциональны ли следующие соотношения: 8:10 и 12:15.
Пояснение
- Умножьте первое и четвертое члены отношений.
8 × 15 = 120
- Теперь умножьте второй и третий член.
10 × 12 = 120
- Поскольку произведение крайностей равно произведению средств,
- Так как произведение средних (120) = произведение крайностей (120),
- Следовательно, 8: 10 и 12:15 пропорциональны.
Пример 2
Убедитесь, что соотношение 6: 12 :: 12: 24 является пропорцией.
Пояснение
- Это случай непрерывной пропорции, поэтому примените формулу a x c = b x b,
- В данном случае a: b: c = 6: 12: 24, следовательно, a = 6, b = 12 и c = 24
- Умножьте первое и третье слагаемые:
6 × 24 = 144
- Квадрат средних членов:
(12) ² = 12 × 12 = 144
- Следовательно, соотношение 6:12:24 пропорционально.
Пример 3
Если 12: 18 :: 20: стр.Найдите значение x, чтобы соотношения были пропорциональными?
Пояснение
Дано: 12: 18 :: 20: p
Приравнять произведение крайностей к произведению средств;
⇒ 12 × p = 20 × 18
⇒ p = (20 × 18) / 12
Решить относительно p;
⇒ p = 30
Следовательно, значение p = 30
Пример 4
Найдите третью пропорцию 3 и 6.
Пояснение
- Пусть третий пропорциональный будет c.
- Тогда b² = ac
6 x 6 = 3 x c
С = 36/3
= 12
Таким образом, третье пропорционально 3 и 6 равно 12
Пример 5
Вычислить среднее пропорциональное от 3 до 27
Пояснение
- Пусть среднее пропорциональное между 3 и 27 будет м.
- Применяя формулу b² = ac; ‘
Следовательно, m x m = 27 x 3 = 81
m 2 = 81
⇒ m = √81
⇒ m = 9
Следовательно, среднее значение, пропорциональное между 3 и 27, равно 9
Пример 6
Учитывая отношения a: b = 4: 5 и b: c = 6: 7, определите соотношение a: b: c.
Пояснение
- Так как b — общий член между двумя отношениями;
- Умножьте каждый член в первом соотношении на значение b во втором соотношении;
a: b = 4: 5 = 24:30,
- Также умножьте каждый член во втором соотношении на значение b в первом соотношении;
b: c = 6: 7 = 30: 35
Следовательно, соотношение a: b: c = 24:30:35
Золотое сечение
Наибольшее применение пропорции — это золотое сечение , которое очень помогло в анализе пропорций различных объектов и искусственных систем, таких как финансовые рынки.Считается, что эти две величины находятся в золотом сечении, если их отношение равно отношению их суммы к большей из двух величин, то есть (a + b) / a = a / b, где a> b> 0.
Это соотношение обозначается греческой буквой φ. Дальнейшее упрощение этого уравнения дает φ 2 — φ — 1 = 0. Решая это по формуле корней квадратного уравнения, мы получаем φ = 1.6180339887…
Евклид и многие математики после него работали над золотым сечением и нашли его существование в правильном пятиугольнике и золотом прямоугольнике.
Практические вопросы
1. Определите значение пропущенной буквы в каждой из следующих пропорций.
а. 6: 9 = ч: 15
г. т: 7 = 12: 21
г. 4: у = 8: 14
г. г: 3 = 0,4: 0,5
e. 1/3 ∶ 1/4 = 1/9:
ф. 9: к = 6: 10
г. 2: 7 = м: 42
ч. 30: 25 = 42: r
я. х: 1,5 = 6,3: 4,5
2. Учитывая первый, второй и четвертый члены в пропорции 9, 21 и 77 соответственно.Вычислите значение третьего члена.
3. Стоимость 4 кг риса 28 долларов. Найдите стоимость 20 кг риса.
4. Отношение длины цветника к ширине 3/2. Рассчитайте длину цветника, если ширина 36 м.
5. В церковном хоре должны быть сформированы группы из мужчин и женщин. Если каждая группа должна состоять из 6 женщин и 4 мужчин. Сколько мужчин требуется, если в церкви 102 женщины?
Ответы
1.
а. 10
г. 4
г. 7
г. 2,4
e. 1/12
ф. 15
г. 12
ч. 35
я. 2,1
2. 33
3. 140 долларов США
4. 54 м
5. 68
Предыдущий урок | Главная страница | Следующий урок
Пропорции и проценты (предварительная алгебра, соотношения и проценты) — Mathplanet
Пропорция — это уравнение, которое говорит, что два или более отношений равны.Например, если один пакет файлов cookie содержит 20 файлов cookie, это будет означать, что 2 пакета содержат 40 файлов cookie
$$ \ frac {20} {1} = \ frac {40} {2} $$
Пропорция читается как «x относится к y, как a относится к b».
$$ \ frac {x} {y} = \ frac {a} {b} $$
$$ \ frac {x} {{\ color {red} {y}}} \ cdot {\ color {red} {y}} = \ frac {a} {b} \ cdot y $$
$$ x \ cdot b = \ frac {a} {{\ color {red} {b}}} \ cdot y {\ color {red} {b}} $$
$$ xb = ay $$
Произведения xb и ay называются перекрестными произведениями.Перекрестные произведения пропорции всегда равны. Если мы хотим проверить, образуют ли два соотношения пропорцию, мы можем просто проверить их перекрестные произведения.
Пример
Используйте перекрестное произведение, чтобы определить, образуют ли два отношения пропорцию.
$$ \ frac {2} {16}, \: \: \ frac {5} {40} $$
$$ \ frac {2} {16} \ overset {?} {=} \ Frac {5} {40} $$
$$ \ frac {2} {16} \ cdot 16 \ cdot 40 \ overset {?} {=} \ Frac {5} {40} \ cdot 16 \ cdot 40 $$
$$ \ frac {2} {{\ color {red} {16}}} \ cdot {\ color {red} {16}} \ cdot 40 \ overset {?} {=} \ Frac {5} {{ \ color {red} {40}}} \ cdot 16 \ cdot {\ color {red} {40}} $$
$$ 2 \ cdot 40 \ overset {?} {=} 5 \ cdot 16 $$
$$ 80 = 80 $$
Здесь мы видим, что 2/16 и 5/40 являются пропорциями, поскольку их перекрестные произведения равны.
Процент означает сотые или сотые и обозначается символом%. Процент — это соотношение, при котором мы сравниваем числа со 100, что означает, что 1% равен 1/100.
Пример
В коробке из восьми пончиков два с розовой посыпкой. Постарайтесь выразить пропорциями, сколько процентов пончиков в коробке с розовой посыпкой.
$$ \ frac {2} {8} = \ frac {x} {100} $$
$$ \ frac {2} {{\ color {red} {8}}} \ cdot {\ color {red} {8}} = \ frac {x} {100} \ cdot 8 $$
$$ 2 \ cdot 100 = \ frac {8x} {{\ color {red} {100}}} \ cdot {\ color {red} {100}} $$
$$ \ frac {200} {8} = \ frac {{\ color {red} {8}} x} {{\ color {red} {8}}} $$
$$ x = 25 \% $$
Эта пропорция называется процентной долей.
$$ \ frac {a} {b} = \ frac {x} {100} $$
Дроби, проценты и десятичные дроби могут представлять одно и то же число, но выражаются по-разному.
Десятичная дробь è процент: Мы можем преобразовать десятичные дроби в проценты, записав десятичную дробь в виде дроби со знаменателем 1. Затем мы увеличиваем дробь на 100, чтобы получить десятичную дробь в процентах.
Пример
Напишите 0,27 в процентах.
$$ 0,27 \ rightarrow \ frac {0,27} {1} \ cdot 100 = \ frac {27} {100} \: \: или \: \: 27 \% $$
Процент è десятичный: запишите процент в виде дроби со знаминателем 100.Следует помнить, что 100% = 1 с
$$ \ frac {100} {100} = 1 $$
Пример
Запишите 89% в виде десятичной дроби.
$$ \ frac {x} {100} = \ frac {89} {100} = 0,89 $$
Видеоурок
Записать в процентах или десятичных дробях
Пропорция населения
— Статистика Как к
Статистические определения> Доля населения
Какова доля населения?
Доля населения — это часть населения , имеющая определенную характеристику.Например, предположим, что у вас 1000 человек в населении, и у 237 из них голубые глаза. Доля людей с голубыми глазами — 237 из 1000, или 237/1000. Буква p используется для обозначения доли населения, поэтому этот факт можно записать так:
p = 237/1000.
Вы также можете записать 237/100 в виде десятичной дроби (разделив 1000 на 237). Если вы это сделали, то p = 0,237.
Диаграмма Венна животных в клинике и «собак», подмножество популяции.
Пример вопроса: Ветеринарная клиника сообщает, что из 3412 животных, зарегистрированных в клинике, 1712 — собаки, 1012 — кошки, а остальные — грызуны или птицы. Какова доля собак в клинике p?
Ответ: Количество собак — 1 712, общее количество — 3 412 голов. Следовательно, p = 1,712 / 3,412. В десятичном формате это p = 1712/3412 = 0,502 (с точностью до двух десятичных знаков).
Формула
Чтобы получить «p», просто разделите общую популяцию (в приведенном выше вопросе это животные в клинике) на количество предметов, которые вас интересуют (в приведенном выше случае это собаки).В виде формулы это записывается как:
p = x / n
Где:
«x» — это количество элементов, которые вас интересуют, а
«n» — это общее количество элементов в генеральной совокупности.
Примечание : Хотя «p» обычно используется в качестве символа доли населения, вы также можете увидеть вместо него букву «пи» (π).
Оценка p
В реальном мире вы обычно не знаете фактов обо всей совокупности, поэтому вы используете выборочные данные для оценки p.Этот образец пропорции записывается как p̂, произносится как p-hat . Он рассчитывается таким же образом, за исключением того, что вы используете данные из выборки: просто разделите общее количество элементов в выборке на количество элементов, которые вас интересуют.
Пример вопроса: При опросе 3121 человека 412 не были вакцинированы. Какая доля недовакцинированных людей среди местного населения?
Ответ: Вы не знаете данных о населении для данной местности, поэтому используйте данные из выборки:
p̂ = x / n
= 412/3121
= 0.132 (до 3 знаков после запятой).
Next : Использование выборки для оценки с.
См. Также: Доверительный интервал для населения. Пропорция.
Список литературы
Гоник Л. (1993). Мультяшный справочник по статистике. HarperPerennial.
Kotz, S .; и др., ред. (2006), Энциклопедия статистических наук, Wiley.
Vogt, W.P. (2005). Словарь статистики и методологии: нетехническое руководство для социальных наук. МУДРЕЦ.
Уилан, К.(2014). Голая статистика. W. W. Norton & Company
————————————————— —————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .

 Далее затарить (взвесить бытовым кантером или бытовыми весами) ведро или другую подходящую емкость наполненную цементом, песком и щебнем (как единицу измерения), и таким образом привести единицу измерения «килограммы» к единице измерения – «ведро/емкость». Теперь можно пользоваться ведром или емкостью для отмера компонентов бетона с учетом указанных выше соотношений.
Далее затарить (взвесить бытовым кантером или бытовыми весами) ведро или другую подходящую емкость наполненную цементом, песком и щебнем (как единицу измерения), и таким образом привести единицу измерения «килограммы» к единице измерения – «ведро/емкость». Теперь можно пользоваться ведром или емкостью для отмера компонентов бетона с учетом указанных выше соотношений.

 Её вместительности должно хватить и для бензина, и для масла.
Её вместительности должно хватить и для бензина, и для масла. Компоненты разбавляют водой, и тщательно перемешивают, чтобы получить однородную массу. Весь состав необходимо израсходовать в течении одного часа, иначе он потеряет своё качество.
Компоненты разбавляют водой, и тщательно перемешивают, чтобы получить однородную массу. Весь состав необходимо израсходовать в течении одного часа, иначе он потеряет своё качество. 