Урок 31. куб суммы. куб разности — Алгебра — 7 класс
Алгебра
7 класс
Урок № 31
Куб суммы. Куб разности
Перечень вопросов, рассматриваемых в теме:
- Формулы сокращённого умножения.
- Куб суммы. Куб разности.
- Разложение многочлена на множители.
- Тождественные преобразования.
- Вычисление значения числовых выражений.
Тезаурус:
Формулы сокращённого умножения.
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
(a + b)(a – b) = a2 – b2
a3 + b3 = (a + b)(a2 – ab + b2)
a3 – b3 = (a – b)(a2 + ab + b2)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a – b)3 = a3 – 3a2b + 3ab2 – b3
Применение:
- упрощение умножения многочленов;
- разложение многочлена на множители;
- вычисление значения числового выражения;
- тождественные преобразования.

Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Куб суммы.
Рассмотрим произведение:
(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b).
Применив правило умножения многочленов, и приведя подобные члены, получим:
a3 + 2a2b + b2a + a2b + 2ab2 + b 3= a3 + 3a2b + 3ab2 + b3.
Итак, доказано равенство, которое называют «куб суммы»: (a + b)3 = a3 + 3a2b + 3ab2 + b3
Читается так: «куб суммы двух чисел равен кубу первого числа, плюс утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, плюс куб второго числа».
Куб разности.
Аналогично докажем формулу «куб разности».
Рассмотрим произведение:
(a – b)3 = (a – b)2(a – b) =(a2 – 2ab + b2)(a – b)
Применив правило умножения многочленов, получим:
a3 – 2a2b + b2a – a2b + 2ab2 – b3 = a3 – 3a2b + 3ab2 – b3
Доказано равенство, которое называют «куб разности»:
(a – b)3 = a3 – 3a2b + 3ab2 – b3
Читается так: «куб разности двух чисел равен кубу первого числа, минус утроенное произведение квадрата первого числа на второе, плюс утроенное произведение первого числа и квадрата второго, минус куб второго числа».
Формулы суммы и разности кубов часто используют для упрощения выражений.
Разбор решения заданий тренировочного модуля.
Задача 1.
Найдите куб двучлена:
(a + 3)3 = a3 + 3a2 · 3 + 3a · 32 + 33 = a3 + 9a2 + 27a + 27.
(10 – a)3 =103 – 3 · 102 a + 3 · 10 · a2 – a3 = 1000 – 300a + 30a2 – a3.
Задача 2.
Упростите: x3 + 3x(x + 4) – (x + 2)3
x3 + 3x2 + 12x – (x3 + 6x2 + 12x + 8) =
x3 + 3x2 + 12x – x3 – 6x2 – 12x – 8 =
= -3x2 – 8.
Ответ: -3x2 – 8.
Задача 3.
Решите уравнение:
x3 + 9x2 – (x + 3)3 = 0
x3 + 9x2 – (x3 + 9x2 + 27x + 27) = 0
x3 + 9x2 – x3 – 9x2 – 27x – 27 = 0
-27x = 27
Ответ: х = -1.
Таблица кубов натуральных чисел от 1 до 209
Число в кубе (в третей степени) это результат умножения заданного числа трижды на самого себя. x3 = x • x • x (если к примеру х=3, то по формуле возведя его в куб, мы получим 33 = 3 • 3 • 3 = 27;
Пример: ab3 = 103 = 1… + …03 = 1000 …
| ab3 | …03 | …13 | …23 | …33 | …43 | …53 | …63 | …73 | …83 | …93 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0… | 0 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 |
| 1… | 1 000 | 1 331 | 1 728 | 2 197 | 2 744 | 3 375 | 4 096 | 4 913 | 5 832 | 6 859 |
| 2… | 8 000 | 9 261 | 10 648 | 12 167 | 13 824 | 15 625 | 17 576 | 19 683 | 21 952 | 24 389 |
| 3… | 27 000 | 29 791 | 32 768 | 35 937 | 39 304 | 42 875 | 46 656 | 50 653 | 54 872 | 59 319 |
| 4… | 64 000 | 68 921 | 74 088 | 79 507 | 85 184 | 91 125 | 97 336 | 103 823 | 110 592 | 117 649 |
| 5… | 125 000 | 132 651 | 140 608 | 148 877 | 157 464 | 166 375 | 175 616 | 185 193 | 195 112 | 205 379 |
| 6… | 216 000 | 226 981 | 238 328 | 250 047 | 262 144 | 274 625 | 287 496 | 300 763 | 314 432 | 328 509 |
| 7… | 343 000 | 357 911 | 373 248 | 389 017 | 405 224 | 421 875 | 438 976 | 456 533 | 474 552 | 493 039 |
| 8… | 512 000 | 531 441 | 551 368 | 571 787 | 592 704 | 614 125 | 636 056 | 658 503 | 681 472 | 704 969 |
| 9… | 729 000 | 753 571 | 778 688 | 804 357 | 830 584 | 857 375 | 884 736 | 912 673 | 941 192 | 970 299 |
| 10… | 1 000 000 | 1 030 301 | 1 061 208 | 1 092 727 | 1 124 864 | 1 157 625 | 1 191 016 | 1 225 043 | 1 259 712 | 1 295 029 |
| 11… | 1 331 000 | 1 367 631 | 1 404 928 | 1 442 897 | 1 481 544 | 1 520 875 | 1 560 896 | 1 601 613 | 1 643 032 | 1 685 159 |
| 12… | 1 728 000 | 1 771 561 | 1 815 848 | 1 860 867 | 1 906 624 | 1 953 125 | 2 000 376 | 2 048 383 | 2 097 152 | 2 146 689 |
| 13… | 2 197 000 | 2 248 091 | 2 299 968 | 2 352 637 | 2 406 104 | 2 460 375 | 2 515 456 | 2 571 353 | 2 628 072 | 2 685 619 |
| 14… | 2 744 000 | 2 803 221 | 2 863 288 | 2 924 207 | 2 985 984 | 3 048 625 | 3 112 136 | 3 176 523 | 3 241 792 | 3 307 949 |
| 15… | 3 375 000 | 3 442 951 | 3 511 808 | 3 581 577 | 3 652 264 | 3 723 875 | 3 796 416 | 3 869 893 | 3 944 312 | 4 019 679 |
| 16… | 4 096 000 | 4 173 281 | 4 251 528 | 4 330 747 | 4 410 944 | 4 492 125 | 4 574 296 | 4 657 463 | 4 741 632 | 4 826 809 |
| 17… | 4 913 000 | 5 000 211 | 5 088 448 | 5 177 717 | 5 268 024 | 5 359 375 | 5 451 776 | 5 545 233 | 5 639 752 | 5 735 339 |
| 18… | 5 832 000 | 5 929 741 | 6 028 568 | 6 128 487 | 6 229 504 | 6 331 625 | 6 434 856 | 6 539 203 | 6 644 672 | 6 751 269 |
| 19… | 6 859 000 | 6 967 871 | 7 077 888 | 7 189 057 | 7 301 384 | 7 414 875 | 7 529 536 | 7 645 373 | 7 762 392 | 7 880 599 |
| 20… | 8 000 000 | 8 120 601 | 8 242 408 | 8 365 427 | 8 489 664 | 8 615 125 | 8 741 816 | 8 869 743 | 8 998 912 | 9 129 329 |
…
Как распечатать таблицу? Левой кнопкой на мишке выделите полностью всё таблицу, на выделенном фоне нажмите правую кнопку мишки и в появившемся меню перейдете в пункт «Печать».
Как пользоваться таблицей? Допустим, что Вам конкретно нужно узнать куб такого двухзначного числа, как 25, для этого в крайней левой вертикальной колонке (отмечена синим цветом) находим строчку с указанием нужных десятков — 2… , после в верхнем горизонтальном рядке ищем пункт …53 , в условном месте пересечении этих двух цифр будет находится правильный ответ, в нашем случае 15625. (Пример: 253= 2… + …53 = 15625)
Автор: Bill4iam
Формулы сокращенного умножения 💣
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 — b2 = (a — b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.
Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2.
Докажем, что a2 — b2 = (a — b) * (a + b).
Поехали:
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a2 — b2 = a2 — b2 + ab — ab
- Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
- Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)
- Вынесем общие множители за скобки:
(a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)
- Вынесем за скобки (a — b).
 a * (a — b) + b * (a — b) = (a — b) * (a + b)
a * (a — b) + b * (a — b) = (a — b) * (a + b) - Результат доказательства: a2 — b2 = (a — b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+ 2 * an-1 * an
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
an − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10)2.
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с3 – 8.
Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y2 — x2.
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Куб суммы и куб разности двух выражений: формула, примеры с решением
Формула куба суммы
Возведем в куб сумму (a+b):
$$ (a+b)^3 = (a+b) (a+b)^2 = (a+b)(a^2+2ab+b^2 ) = $$
$$ = a(a^2+2ab+b^2 )+b(a^2+2ab+b^2 ) = a^3+2a^2 b+ab^2+a^2 b+2ab^2+b^3 = $$
$$ = a^3+3a^2 b+3ab^2+b^3 $$
Мы получили формулу куба суммы двух выражений:
$$(a+b)^3 = a^3+3a^2 b+3ab^2+b^3$$
Куб суммы двух выражений равен кубу первого выражения, плюс утроенное произведение квадрата первого выражения на второе выражение, плюс утроенное произведение первого выражения на квадрат второго выражения, плюс куб второго выражения. 3$
3$
Формулы сокращённого умножения
- Главная
- Алгебра
- Одночлены, многочлены, формулы сокращённого умножения.
- Формулы сокращённого умножения
Квадрат суммы двух чисел
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого на второе плюс квадрат второго числа.
( x + y )2 = x2 + 2 × x × y + y2
10042 = 1000000 + 8000 + 16 = 1008016
Квадрат разности двух чисел
Квадрат разности двух чисел равен квадрату первого числа, минус удвоенное произведение первого на второе плюс квадрат второго числа.
( x — y )2 = x2 — 2 × x × y + y2
9972 = 1000000 — 6000 + 9 = 994009
Куб суммы двух чисел
Куб суммы двух чисел равен кубу первого числа ПЛЮС утроенное произведение квадрата первого на второе, ПЛЮС утроенное произведение первого на квадрат второго ПЛЮС куб второго числа.
( x + y )3 = x3 + 3 × x2 × y + 3 × x × y2 + y3
Куб разности двух чисел
Куб разности двух чисел равен кубу первого числа МИНУС утроенное произведение квадрата первого на второе ПЛЮС утроенное произведение первого на квадрат второго МИНУС куб второго числа.
( x — y )3 = x3 — 3 × x2 × y + 3 × x × y2 — y3
Разность квадратов двух чисел
Разность квадратов двух чисел равна произведению их суммы на разность.
x2 — y2 = ( x + y ) × ( x — y )
1003 × 997 = 1000000 — 9 = 999991
Сумма кубов двух чисел
Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности.
x3 + y3 = ( x + y ) × ( x2 — x × y + y2 )
Разность кубов двух чисел
Разность кубов двух чисел равна произведению разности этих чисел на неполный квадрат их суммы.
x3 — y3 = ( x — y ) × ( x2 + x × y + y2 )
Квадрат многочлена
Квадрат многочлена равен сумме квадратов всех его слагаемых плюс удвоенные произведения всех пар разных слагаемых.
Формулы сокращенного умножения
Продолжаем изучать многочлены. В данном уроке мы научимся перемножать многочлены с помощью формул сокращённого умножения.
Предварительные навыки
Квадрат суммы двух выражений
Существует ряд случаев, когда умножение многочлена на многочлен можно значительно упростить. Таковым к примеру является случай (2x + 3y)2.
Выражение (2x + 3y)2 это перемножение двух многочленов, каждый из которых равен (2x + 3y)
(2x + 3y)2 = (2x + 3y)(2x + 3y)
Получили умножение многочлена на многочлен. Выполним его:
(2x + 3y)2 = (2x + 3y)(2x + 3y) = 4x2 + 6xy + 6xy + 9y2 = 4x2 + 12xy + 9y2
То есть выражение (2x + 3y)2 равно 4x2 + 12xy + 9y2
(2x + 3y)2 = 4x2 + 12xy + 9y2
Решим аналогичный пример, который попроще:
(a + b)2
Выражение (a + b)2 это перемножение двух многочленов, каждый из которых равен (a + b)
(a + b)2 = (a + b)(a + b)
Выполним это умножение:
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
То есть выражение (a + b)2 равно a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2
Оказывается, что случай (a + b)2 можно распространить для любых a и b.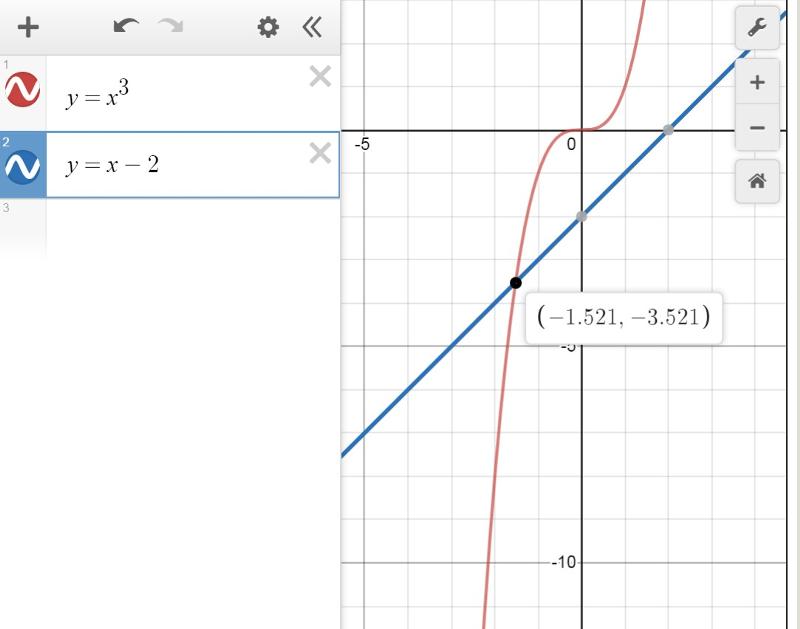 Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y
Первый пример, который мы решили, а именно (2x + 3y)2 можно решить с помощью тождества (a + b)2 = a2 + 2ab + b2. Для этого нужно подставить вместо переменных a и b соответствующие члены из выражение (2x + 3y)2. В данном случае переменной a соответствует член 2x, а переменной b соответствует член 3y
a = 2x
b = 3y
И далее можно воспользоваться тождеством (a + b)2 = a2 + 2ab + b2, но вместо переменных a и b нужно подставлять выражения 2x и 3y соответственно:
(2x + 3y)2 = (2x)2 + 2 × 2x × 3y + (3y)2 = 4x2 + 12xy + 9y2
Как и в прошлый раз получили многочлен 4x2 + 12xy + 9y2.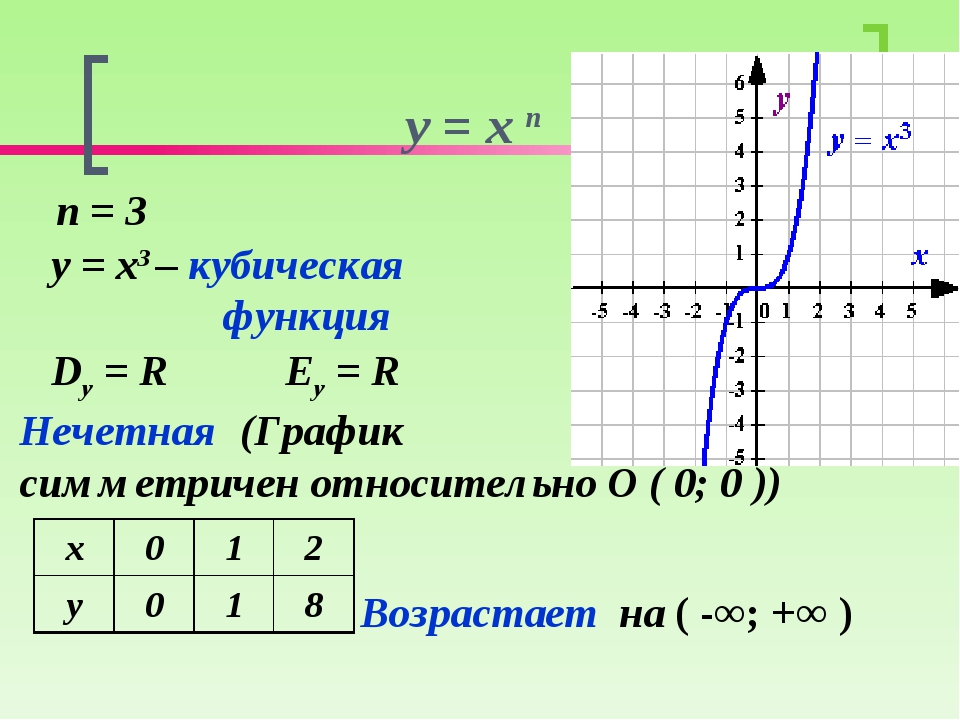 Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
Решение обычно записывают покороче, выполняя в уме все элементарные преобразования:
(2x + 3y)2 = 4x2 + 12xy + 9y2
Тождество (a + b)2 = a2 + 2ab + b2 называют формулой квадрата суммы двух выражений. Эту формулу можно прочитать так:
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Рассмотрим выражение (2 + 3)2. Его можно вычислить двумя способами: выполнить сложение в скобках и возвести полученный результат в квадрат, либо воспользоваться формулой квадрата суммы двух выражений.
Первый способ:
(2 + 3)2 = 52 = 25
Второй способ:
(2 + 3)2 = 22 + 2 × 2 × 3 + 32 = 4 + 12 + 9 = 25
Пример 2. Преобразовать выражение (5a + 3)2 в многочлен.
Преобразовать выражение (5a + 3)2 в многочлен.
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
(5a + 3)2 = (5a)2 + 2 × 5a × 3 + 32 = 25a2 + 30a + 9
Значит, (5a + 3)2 = 25a2 + 30a + 9.
Попробуем решить данный пример, не пользуясь формулой квадрата суммы. У нас должен получиться тот же результат:
(5a + 3)2 = (5a + 3)(5a + 3) = 25a2 + 15a + 15a + 9 = 25a2 + 30a + 9
Формула квадрата суммы двух выражений имеет геометрический смысл. Мы помним, что для вычисления площади квадрата нужно возвести во вторую степень его сторону.
Например, площадь квадрата со стороной a будет равна a2.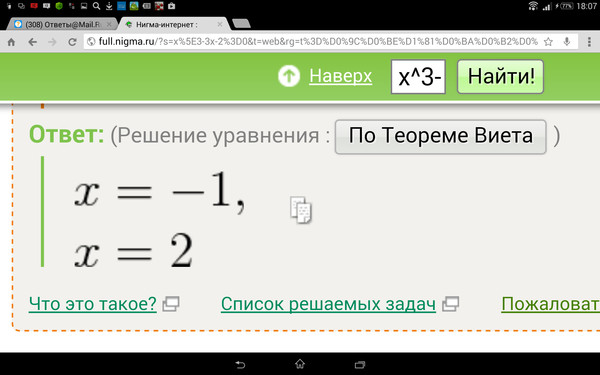 Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Если увеличить сторону квадрата на b, то площадь будет равна (a + b)2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке увеличили на b. У квадрата все стороны равны. Если его сторону увеличить на b, то остальные стороны тоже увеличатся на b
Получился новый квадрат, который больше предыдущего. Чтобы хорошо увидеть его, достроим отсутствующие стороны:
Чтобы вычислить площадь этого квадрата, можно по отдельности вычислить квадраты и прямоугольники, входящие в него, затем сложить полученные результаты.
Сначала можно вычислить квадрат со стороной a — его площадь будет равна a2. Затем можно вычислить прямоугольники со сторонами a и b — они будут равны ab. Затем можно вычислить квадрат со стороной b
В результате получается следующая сумма площадей:
a2 + ab + ab + b2
Сумму площадей одинаковых прямоугольников можно заменить на умножение 2ab, которое буквально будет означать «повторить два раза площадь прямоугольника ab». Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
Алгебраически это получается путём приведения подобных слагаемых ab и ab. В результате получается выражение a2 + 2ab + b2, которое является правой частью формулы квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Квадрат разности двух выражений
Формула квадрата разности двух выражений выглядит следующим образом:
(a − b)2 = a2 − 2ab + b2
Эту формулу можно прочитать так:
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Формула квадрата разности двух выражений выводится таким же образом, как и формула квадрата суммы двух выражений. Выражение (a − b)2 представляет собой произведение двух многочленов, каждый из которых равен (a − b)
(a − b)2 = (a − b)(a − b)
Если выполнить это умножение, то получится многочлен a2 − 2ab + b2
(a − b)2 = (a − b)(a − b) = a2 − ab − ab + b2 = a2 − 2ab + b2
Пример 1. Преобразовать выражение (7x − 5)2 в многочлен.
Преобразовать выражение (7x − 5)2 в многочлен.
Воспользуемся формулой квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
(7x − 5)2 = (7x)2 − 2 × 7x × 5 + 52 = 49x2 − 70x + 25
Значит, (7x − 5)2 = 49x2 − 70x + 25.
Попробуем решить данный пример, не пользуясь формулой квадрата разности. У нас должен получиться тот же результат:
(7x − 5)2 = (7x − 5)(7x − 5) = 49x2 − 35x − 35x + 25 = 49x2 − 70x + 25.
Формула квадрата разности двух выражений тоже имеет геометрический смысл. Если площадь квадрата со стороной a равна a2, то площадь квадрата, сторона которого уменьшена на b, будет равна (a − b)2
Рассмотрим следующий рисунок:
Представим, что сторону квадрата, изображённого на данном рисунке уменьшили на b. У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
У квадрата все стороны равны. Если одну сторону уменьшить на b, то остальные стороны тоже уменьшатся на b
Получился новый квадрат, который меньше предыдущего. На рисунке он выделен жёлтым. Сторона его равна a − b, поскольку старая сторона a уменьшилась на b. Чтобы вычислить площадь этого квадрата, можно из первоначальной площади квадрата a2 вычесть площади прямоугольников, которые получились в процессе уменьшения сторон старого квадрата. Покажем эти прямоугольники:
Тогда можно написать следующее выражение: старая площадь a2 минус площадь ab минус площадь (a − b)b
a2 − ab − (a − b)b
Раскроем скобки в выражении (a − b)b
a2 − ab − ab + b2
Приведем подобные слагаемые:
a2 − 2ab + b2
В результате получается выражение a2 − 2ab + b2, которое является правой частью формулы квадрата разности двух выражений:
(a − b)2 = a2 − 2ab + b2
Формулы квадрата суммы и квадрата разности в общем называют формулами сокращённого умножения. Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Эти формулы позволяют значительно упростить и ускорить процесс перемножения многочленов.
Ранее мы говорили, что рассматривая член многочлена по отдельности, его нужно рассматривать вместе со знаком, который перед ним располагается.
Но применяя формулы сокращённого умножения, знак исходного многочлена не следует рассматривать в качестве знака самого этого члена.
Например, если дано выражение (5x − 2y)2, и мы хотим воспользоваться формулой (a − b)2 = a2 − 2ab + b2, то вместо b нужно подставлять 2y, а не −2y. Это особенность работы с формулами, которую не следует забывать.
(5x − 2y)2
a = 5x
b = 2y
(5x − 2y)2 = (5x)2 − 2 × 5x × 2y + (2y)2 = 25x2 − 20xy + 4y2
Если подставлять −2y, то это будет означать, что разность в скобках исходного выражения была заменена на сумму:
(5x − 2y)2 = (5x + (−2y))2
и в таком случае нужно применять не формулу квадрата разности, а формулу квадрата суммы:
(5x + (−2y)2
a = 5x
b = −2y
(5x + (−2y))2 = (5x)2 + 2 × 5x × (−2y) + (−2y)2 = 25x2 − 20xy + 4y2
Исключением могут быть выражения вида (x − (−y))2. В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
В данном случае, применяя формулу (a − b)2 = a2 − 2ab + b2 вместо b следует подставить (−y)
(x − (−y))2 = x2 − 2 × x × (−y) + (−y)2 = x2 + 2xy + y2
Но возводя в квадрат выражения вида x − (−y), удобнее будет заменять вычитание на сложение x + y. Тогда первоначальное выражение примет вид (x + y)2 и можно будет воспользоваться формулой квадрата суммы, а не разности:
(x + y)2 = x2 + 2xy + y2
Куб суммы и куб разности
Формулы куба суммы двух выражений и куба разности двух выражений выглядят следующим образом:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a − b)3 = a3 − 3a2b + 3ab2 − b3
Формулу куба суммы двух выражений можно прочитать так:
Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
А формулу куба разности двух выражений можно прочитать так:
Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
При решении задач желательно знать эти формулы наизусть. Если не запомнили — не беда! Их можно выводить самостоятельно. Мы это уже умеем.
Выведем формулу куба суммы самостоятельно:
(a + b)3
Выражение (a + b)3 представляет собой произведение из трёх многочленов, каждый из которых равен (a + b)
(a + b)3 = (a + b)(a + b)(a + b)
Но выражение (a + b)3 также может быть записано как (a + b)(a + b)2
(a + b)3 = (a + b)(a + b)2
При этом сомножитель (a + b)2 является квадратом суммы двух выражений. Этот квадрат суммы равен выражению a2 + 2ab + b2.
Этот квадрат суммы равен выражению a2 + 2ab + b2.
Тогда (a + b)3 можно записать как (a + b)(a2 + 2ab + b2).
(a + b)3 = (a + b)(a2 + 2ab + b2)
А это есть умножение многочлена на многочлен. Выполним его:
(a + b)3 = (a + b)(a2 + 2ab + b2) = a3 + 2a2b + ab2 + a2b + 2ab2 + b3 = a3 + 3a2b + 3ab2 + b3
Аналогично можно вывести формулу куба разности двух выражений:
(a − b)3 = (a − b)(a2 − 2ab + b2) = a3 − 2a2b + ab2 − a2b + 2ab2 − b3 = a3 − 3a2b + 3ab2 − b3
Пример 1. Преобразуйте выражение (x + 1)3 в многочлен.
Преобразуйте выражение (x + 1)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(x + 1)3 = x3 + 3 × x2 × 1 + 3 × x × 12 + 13 = x3 + 3x2 + 3x + 1
Попробуем решить данный пример, не используя формулу куба суммы двух выражений. У нас получится тот же результат, но решение станет длиннее:
(x + 1)3 = (x + 1)(x + 1)(x + 1) = (x + 1)(x2 + 2x + 1) = x3 + 2x2 + x + x2 + 2x + 1 = x3 + 3x2 + 3x + 1
Пример 2.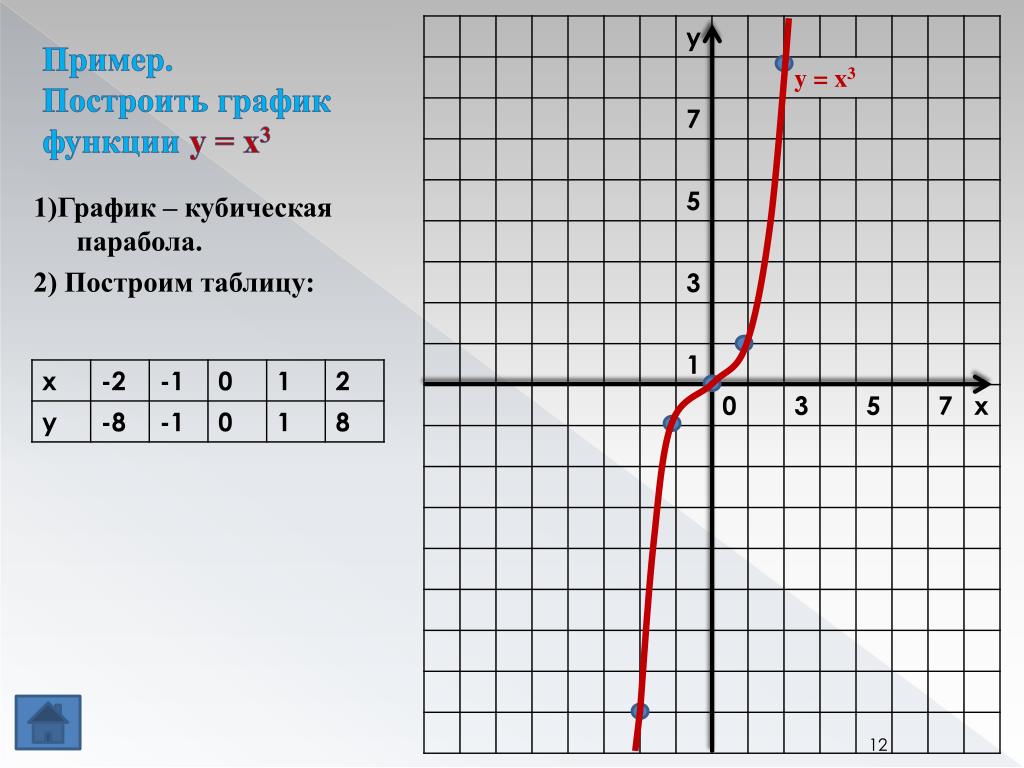 Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Преобразовать выражение (6a2 + 3b3)3 в многочлен.
Воспользуемся формулой куба суммы двух выражений:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(6a2 + 3b3)3= (6a2)3 + 3 × (6a2)2 × 3b3 + 3 × 6a2 × (3b3)2 + (3b3)3 = 216a6 + 3 × 36a4 × 3b3 + 3 × 6a2 × 9b6 + 27b9
Пример 3. Преобразовать выражение (n2 − 3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(n2 − 3)3 = (n2)3 − 3 × (n2)2 × 3 + 3 × n2 × 32 − 33 = n6 − 9n4 + 27n2 − 27
Пример 4. Преобразовать выражение (2x2 − x3)3 в многочлен.
Преобразовать выражение (2x2 − x3)3 в многочлен.
Воспользуемся формулой куба разности двух выражений:
(a − b) = a3 − 3a2b + 3ab2 − b3
(2x2 − x3)3 = (2x2)3 − 3 × (2x2)2 × x3 + 3 × 2x2 × (x3)2 − (x3)3 =
8x6 − 3 × 4x4 × x3 + 3 × 2x2 × x6 − x9 =
8x6 − 12x7 + 6x8 − x9
Умножение разности двух выражений на их сумму
Встречаются задачи, в которых требуется умножить разность двух выражений на их сумму. Например:
Например:
(a − b)(a + b)
В этом выражении разность двух выражений a и b умножена на сумму этих же двух выражений. Выполним данное умножение:
(a − b)(a + b) = a2 + ab − ab − b2 = a2 − b2
То есть выражение (a − b)(a + b) равно a2 − b2
(a − b)(a + b) = a2 − b2
Видим, что при умножении разности двух выражений на их сумму, получается разность квадратов этих выражений.
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений.
Случай (a − b)(a + b) можно распространить для любых a и b. Проще говоря, если при решении задачи потребуется умножить разность двух выражений на их сумму, то это умножение можно заменить на разность квадратов этих выражений.
Пример 1. Выполнить умножение (2x − 5)(2x + 5)
В этом примере разность выражений 2x и 5 умножена на сумму этих же выражений. Тогда согласно формуле (a − b)(a + b) = a2 − b2 имеем:
(2x − 5)(2x + 5) = (2x)2 − 52
Вычислим правую часть, получим 4x2 − 25
(2x − 5)(2x + 5) = (2x)2 − 52 = 4x2 − 25
Попробуем решить данный пример, не пользуясь формулой (a − b)(a + b) = a2 − b2. У нас получится тот же результат 4x2 − 25
(2x − 5)(2x + 5) = 4x2 − 10x + 10x − 25 = 4x2 − 25
Пример 2. Выполнить умножение (4x − 5y)(4x + 5y)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(4x − 5y)(4x + 5y) = (4x)2 − (5y)2 = 16x2 − 25y2
Пример 3. Выполнить умножение (2a + 3b)(2a − 3b)
Выполнить умножение (2a + 3b)(2a − 3b)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(2a + 3b)(2a − 3b) = (2a)2 − (3b)2 = 4a2 − 9b2
В данном примере сумма членов 2a и 3b располагалась раньше, чем разность этих членов. А в формуле (a − b)(a + b) = a2 − b2 разность располагается раньше.
Нет никакой разницы как располагаются сомножители (a − b) в (a + b) в формуле. Они могут быть быть записаны как (a − b)(a + b), так и (a + b)(a − b). Результат по прежнему будет равен a2 − b2, поскольку от перестановки сомножителей произведение не меняется.
Так и в данном примере сомножители (2a + 3b) и (2a − 3b) можно записать как (2a + 3b)(2a − 3b), так и (2a − 3b)(2a + 3b). Результат всё так же будет равен 4a2 − 9b2.
Пример 3. Выполнить умножение (7 + 3x)(3x − 7)
Воспользуемся формулой умножения разности двух выражений на их сумму:
(a − b)(a + b) = a2 − b2
(7 + 3x)(3x − 7) = (3x)2 − 72 = 9x2 − 49
Пример 4. Выполнить умножение (x2 − y3)(x2 + y3)
(a − b)(a + b) = a2 − b2
(x2 − y3)(x2 + y3) = (x2)2 − (y3)2 = x4 − y6
Пример 5. Выполнить умножение (−5x − 3y)(5x − 3y)
Выполнить умножение (−5x − 3y)(5x − 3y)
В выражении (−5x − 3y) вынесем за скобки −1, тогда исходное выражение примет следующий вид:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y)
Произведение (5x + 3y)(5x − 3y) заменим на разность квадратов:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2)
Разность квадратов была заключена в скобки. Если этого не сделать, то получится, что −1 умножается только на (5x)2. А это приведет к ошибке и изменению значения исходного выражения.
Далее вычисляем выражение в скобках:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) = −1(25x2 − 9y2)
Теперь умножим −1 на выражение в скобках и получим окончательный результат:
(−5x − 3y)(5x − 3y) = −1(5x + 3y)(5x − 3y) = −1((5x)2 − (3y)2) =
−1(25x2 − 9y2) = −25x2 + 9y2
Умножение разности двух выражений на неполный квадрат их суммы
Встречаются задачи, в которых требуется умножить разность двух выражений на неполный квадрат их суммы. Выглядит это произведение следующим образом:
Выглядит это произведение следующим образом:
(a − b)(a2 + ab + b2)
Первый многочлен (a − b) является разностью двух выражений, а второй многочлен (a2 + ab + b2) является неполным квадратом суммы этих двух выражений.
Неполный квадрат суммы это многочлен вида a2 + ab + b2. Он похож на обычный квадрат суммы a2 + 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 + 6xy + 9y2 является неполным квадратом суммы выражений 2x и 3y.
Действительно, первый член выражения 4x2 + 6xy + 9y2, а именно 4x2 является квадратом выражения 2x, поскольку (2x)2 = 4x2. Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Третий член выражения 4x2 + 6xy + 9y2, а именно 9y2 является квадратом выражения 3y, поскольку (3y)2 = 9y2. Член находящийся в середине 6xy, является произведением выражений 2x и 3y.
Итак, умножим разность (a − b) на неполный квадрат суммы a2 + ab + b2
(a − b)(a2 + ab + b2) = a(a2 + ab + b2) − b(a2 + ab + b2) =
a3 + a2b + ab2 − a2b − ab2 − b3 = a3 − b3
То есть выражение (a − b)(a2 + ab + b2) равно a3 − b3
(a − b)(a2 + ab + b2) = a3 − b3
Это тождество называют формулой умножения разности двух выражений на неполный квадрат их суммы. Эту формулу можно прочитать так:
Эту формулу можно прочитать так:
Произведение разности двух выражений и неполного квадрата их суммы равно разности кубов этих выражений.
Пример 1. Выполнить умножение (2x − 3y)(4x2 + 6xy + 9y2)
Первый многочлен (2x − 3y) это разность двух выражений 2x и 3y. Второй многочлен 4x2 + 6xy + 9y2 это неполный квадрат суммы двух выражений 2x и 3y. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3. В нашем случае умножение (2x − 3y)(4x2 + 6xy + 9y2) можно заменить на разность кубов 2x и 3y
(2x − 3y)(4x2 + 6xy + 9y2) = (2x)3 − (3y)3 = 8x3 − 27y3
Попробуем решить этот же пример, не пользуясь формулой (a − b)(a2 + ab + b2) = a3 − b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x − 3y)(4x2 + 6xy + 9y2) = 2x(4x2 + 6xy + 9y2) − 3y(4x2 + 6xy + 9y2) =
8x3 + 12x2y + 18xy2 − 12x2y − 18xy2 − 27y3 = 8x3 − 27y3
Пример 2. Выполнить умножение (3 − x)(9 + 3x + x2)
Первый многочлен (3 − x) является разностью двух выражений, а второй многочлен является неполным квадратом суммы этих двух выражений. Это позволяет воспользоваться формулой (a − b)(a2 + ab + b2) = a3 − b3
(3 − x)(9 + 3x + x2) = 33 − x3 = 27 − x3
Умножение суммы двух выражений на неполный квадрат их разности
Встречаются задачи, в которых требуется умножить сумму двух выражений на неполный квадрат их разности. Выглядит это произведение следующим образом:
Выглядит это произведение следующим образом:
(a + b)(a2 − ab + b2)
Первый многочлен (a + b) является суммой двух выражений, а второй многочлен (a2 − ab + b2) является неполным квадратом разности этих двух выражений.
Неполный квадрат разности это многочлен вида a2 − ab + b2. Он похож на обычный квадрат разности a2 − 2ab + b2 за исключением того, что в нём произведение первого и второго выражений не удваивается.
Например, выражение 4x2 − 6xy + 9y2 является неполным квадратом разности выражений 2x и 3y.
(2x)2 − 2x × 3y + (3y)2 = 4x2 − 6xy + 9y2
Вернёмся к изначальному примеру. Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
Умножим сумму a + b на неполный квадрат разности a2 − ab + b2
(a + b)(a2 − ab + b2) = a(a2 − ab + b2) + b(a2 − ab + b2) =
a3 − a2b + ab2 + a2b − ab2 + b3 = a3 + b3
То есть выражение (a + b)(a2 − ab + b2) равно a3 + b3
(a + b)(a2 − ab + b2) = a3 + b3
Это тождество называют формулой умножения суммы двух выражений на неполный квадрат их разности. Эту формулу можно прочитать так:
Произведение суммы двух выражений и неполного квадрата их разности равно сумме кубов этих выражений.
Пример 1. Выполнить умножение (2x + 3y)(4x2 − 6xy + 9y2)
Первый многочлен (2x + 3y) это сумма двух выражений 2x и 3y, а второй многочлен 4x2 − 6xy + 9y2 это неполный квадрат разности этих выражений. Это позволяет не приводя длинных вычислений, воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3. В нашем случае умножение (2x + 3y)(4x2 − 6xy + 9y2) можно заменить на сумму кубов 2x и 3y
(2x + 3y)(4x2 − 6xy + 9y2) = (2x)3 + (3y)3 = 8x3 + 27y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x + 3y)(4x2 − 6xy + 9y2) = 2x(4x2 − 6xy + 9y2) + 3y(4x2 − 6xy + 9y2) =
8x3 − 12x2y + 18xy2 + 12x2y − 18xy2 + 27y3 = 8x3 + 27y3
Пример 2. Выполнить умножение (2x + y)(4x2 − 2xy + y2)
Первый многочлен (2x + y) является суммой двух выражений, а второй многочлен (4x2 − 2xy + y2) является неполным квадратом разности этих выражений. Это позволяет воспользоваться формулой (a + b)(a2 − ab + b2) = a3 + b3
(2x + y)(4x2 − 2xy + y2) = (2x)3 + y3 = 8x3 + y3
Попробуем решить этот же пример, не пользуясь формулой (a + b)(a2 − ab + b2) = a3 + b3. У нас получится тот же результат, но решение станет длиннее:
У нас получится тот же результат, но решение станет длиннее:
(2x + y)(4x2 − 2xy + y2) = 2x(4x2 − 2xy + y2) + y(4x2 − 2xy + y2) =
8x3 − 4x2y + 2xy2 + 4x2y − 2xy2 + y3 = 8x3 + y3
Задания для самостоятельного решения
Задание 1. Преобразуйте выражение (m + n)2 в многочлен.
Решение:
(m + n)2 = m2 + 2mn + n2
Задание 2. Преобразуйте выражение (x + 8)2 в многочлен.
Решение:
(x + 8)2 = x2 + 2 × x × 8 + 82 = x2 + 16x + 64
Задание 3. Преобразуйте выражение (2x2 + 3x3)2 в многочлен.
Преобразуйте выражение (2x2 + 3x3)2 в многочлен.
Решение:
(2x2 + 3x3)2 = (2x2)2 + 2 × 2x2 × 3x3 + (3x3)2 = 4x4 + 12x5 + 9x6
Задание 4. Преобразуйте выражение (5a + 5)2 в многочлен.
Решение:
(5a + 5)2 = (5a)2 + 2 × 5a × 5 + 52 = 25a2 + 50a + 25
Задание 5. Преобразуйте выражение (9 − x)2 в многочлен.
Решение:
(9 − x)2 = 92 − 2 × 9 × x + x2 = 81 − 18x + x2
Задание 6. Преобразуйте выражение (x − 25)2 в многочлен.
Решение:
(x − 25)2 = x2 − 2 × x × 25 + 252 = x2 − 50x + 625
Задание 7. Преобразуйте выражение (3x2 − y3)2 в многочлен.
Преобразуйте выражение (3x2 − y3)2 в многочлен.
Решение:
(3x2 − y3)2 = (3x2)2 − 2 × 3x2 × y3 + ( y3)2 = 9x4 − 6x2y3 + y6
Задание 8. Выполните умножение (x − y)(x + y)
Решение:
(x − y)(x + y) = x2 − y2
Задание 9. Выполните умножение (2x − y)(2x + y)
Решение:
(2x − y)(2x + y) = (2x)2 − y2 = 4x2 − y2
Задание 10. Выполните умножение (7 + 3y)(3y − 7)
Решение:
(7 + 3y)(3y − 7) = (3y)2 − 72 = 9y2 − 49
Задание 11. Выполните умножение (x2 − 5)(x2 + 5)
Выполните умножение (x2 − 5)(x2 + 5)
Решение:
(x2 − 5)(x2 + 5) = (x2)2 − 52 = x4 − 25
Задание 12. Выполните умножение (a3 − b2)(a3 + b2)
Решение:
(a3 − b2)(a3 + b2) = (a3)2 − (b2)2 = a6 − b4
Задание 13. Выполните умножение (5a2 + 2b3)(5a2 − 2b3)
Решение:
(5a2 + 2b3)(5a2 − 2b3) = (5a2)2 − (2b3)2 = 25a4 − 4b6
Задание 14. Выполните умножение (9x − y2)(y2 + 9x)
Выполните умножение (9x − y2)(y2 + 9x)
Решение:
(9x − y2)(y2 + 9x) = (9x)2 − (y2)2 = 81x2 − y4
Задание 15. Выполните умножение (2 − x)(4 + 2x + x2)
Решение:
(2 − x)(4 + 2x + x2) = 23 − x3 = 8 − x3
Задание 16. Выполните умножение (3 − 2)(9 + 6 + 4)
Решение:
(3 − 2)(9 + 6 + 4) = 33 − 23 = 27 − 8 = 19
Задание 17. Выполните умножение (4x + 1)(16x2 − 4x + 1)
Решение:
(4x + 1)(16x2 − 4x + 1) = (4x)3 + 13 = 64x3 + 1
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Таблица кубов
Куб числа — есть данное число, возведенное в третью степень. «Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.
«Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.
| 1 3 = 1 2 3 = 8 3 3 = 27 4 3 = 64 5 3 = 125 6 3 = 216 7 3 = 343 8 3 = 512 9 3 = 729 10 3 = 1000 | 11 3 = 1331 12 3 = 1728 13 3 = 2197 14 3 = 2744 15 3 = 3375 16 3 = 4096 17 3 = 4913 18 3 = 5832 19 3 = 6859 20 3 = 8000 | 21 3 = 9261 22 3 = 10648 23 3 = 12167 24 3 = 13824 25 3 = 15625 26 3 = 17576 27 3 = 19683 28 3 = 21952 29 3 = 24389 30 3 = 27000 | 31 3 = 29791 32 3 = 32768 33 3 = 35937 34 3 = 39304 35 3 = 42875 36 3 = 46656 37 3 = 50653 38 3 = 54872 39 3 = 59319 40 3 = 64000 | 41 3 = 68921 42 3 = 74088 43 3 = 79507 44 3 = 85184 45 3 = 91125 46 3 = 97336 47 3 = 103823 48 3 = 110592 49 3 = 117649 50 3 = 125000 |
| 51 3 = 132651 52 3 = 140608 53 3 = 148877 54 3 = 157464 55 3 = 166375 56 3 = 175616 57 3 = 185193 58 3 = 195112 59 3 = 205379 60 3 = 216000 | 61 3 = 226981 62 3 = 238328 63 3 = 262144 64 3 = 262144 65 3 = 274625 66 3 = 287496 67 3 = 300763 68 3 = 314432 69 3 = 328509 70 3 = 343000 | 71 3 = 357911 72 3 = 373248 73 3 = 389017 74 3 = 405224 75 3 = 421875 76 3 = 438976 77 3 = 456533 78 3 = 474552 79 3 = 493038 80 3 = 512000 | 81 3 = 531441 82 3 = 551368 83 3 = 571787 84 3 = 592704 85 3 = 614125 86 3 = 636056 87 3 = 658503 88 3 = 681472 89 3 = 704969 90 3 = 729000 | 91 3 = 753571 92 3 = 778688 93 3 = 804357 94 3 = 830584 95 3 = 857375 96 3 = 884736 97 3 = 912673 98 3 = 941192 99 3 = 970299 100 3 = 1000000 |
Другие заметки по алгебре и геометрии
Как возвести в куб биномы | Sciencing
Алгебра полна повторяющихся шаблонов, которые каждый раз можно вычислить с помощью арифметики. Но поскольку эти шаблоны очень распространены, обычно есть какая-то формула, которая помогает упростить вычисления. Куб бинома — отличный пример: если бы вам приходилось решать его каждый раз, вы бы потратили много времени на работу с карандашом и бумагой. Но как только вы знаете формулу для решения этого куба (и несколько удобных приемов для ее запоминания), найти свой ответ так же просто, как вставить правильные термины в правильные ячейки переменных.
TL; DR (слишком долго; не читал)
Формула для куба бинома ( a + b ):
( a + b ) 3 = a 3 + 3_a_ 2 b + 3_ab_ 2 + b 3
Расчет куба бинома
Нет нужды паниковать, когда вы видите проблему типа (a + б) 3 перед вами.Как только вы разделите его на знакомые компоненты, он начнет выглядеть как более знакомые математические задачи, которые вы уже решали раньше.
В этом случае полезно вспомнить, что
(a + b) (a + b) (a + b) , который должен выглядеть намного более знакомым.
Но вместо того, чтобы каждый раз заниматься математикой с нуля, вы можете использовать «ярлык» формулы, которая представляет ответ, который вы получите. Вот формула для куба бинома:
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Чтобы использовать формулу, определить, какие числа (или переменные) занимают места для «a» и «b» в левой части уравнения, затем подставьте те же числа (или переменные) в слоты «a» и «b» в правой части формула.
Пример 1: Решить (x + 5) 3
Как видите, x занимает слот «a» в левой части формулы, а 5 — слот «b» . Подставив x и 5 в правую часть формулы, вы получите:
Небольшое упрощение приблизит вас к ответу:
x 3 + 3 (5) x 2 + 3 (25) x + 125
И, наконец, как только вы максимально упростили:
А как насчет вычитания?
Вам не нужна другая формула для решения такой задачи, как (y — 3) 3 .Если вы помните, что y — 3 совпадает с y + (-3) , вы можете просто переписать задачу на [y + (-3)] 3 и решить ее, используя знакомую формулу.
Пример 2: Решить (y — 3) 3
Как уже говорилось, ваш первый шаг — переписать задачу на [y + (-3)] 3 .
Затем запомните формулу для куба бинома:
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
In ваша проблема, y занимает слот «a» в левой части уравнения, а -3 занимает слот «b».Подставьте их в соответствующие ячейки в правой части уравнения, обращая особое внимание на скобки, чтобы сохранить отрицательный знак перед -3. Это дает вам:
y 3 + 3y 2 (-3) + 3y (-3) 2 + (-3) 3
Теперь пора упростить. Опять же, обратите особое внимание на этот отрицательный знак при применении экспонент:
y 3 + 3 (-3) y 2 + 3 (9) y + (-27)
Еще один раунд упрощения дает вам ответ:
Следите за суммой и разницей кубов
Всегда обращайте пристальное внимание на то, где находятся показатели степени в вашей задаче.Если вы видите проблему в форме (a + b) 3 или [a + (-b)] 3 , то обсуждаемая здесь формула является подходящей. Но если ваша проблема выглядит как (a 3 + b 3 ) или (a 3 — b 3 ) , это не куб бинома. Это сумма кубиков (в первом случае) или разность кубиков (во втором случае), и в этом случае вы применяете одну из следующих формул:
(a 3 + b 3 ) = ( a + b) (a 2 — ab + b 2 )
(a 3 — b 3 ) = (a — b) (a 2 + ab + b 2 )
Факторизация разностей кубов по формуле.3
$$
Калькулятор кубического корня — Калькулятор капитана
Калькулятор кубического корня
Обратите внимание: для работы этого калькулятора требуется JavaScript.
Определение — Что такое кубический корень?
Кубический корень числа — это число, которое при трехкратном умножении на само себя (число x число x число) дает исходное число.
Например, кубический корень из 27 равен 3, так как 3 x 3 x 3 = 27.
Кубический корень из 125 равен 5, так как 5 x 5 x 5 = 125.
В отличие от квадратного корня, кубический корень всегда положителен.
Корень, противоположный кубу, вычисляется в кубе (степень 3).
В геометрии кубический корень можно использовать для определения длины стороны куба, когда известен объем.
Формула
— Как вычислить кубический корень числа
Нет быстрой формулы для вычисления кубического корня. Большинство калькуляторов используют метод проб и ошибок.
Пробная версия и ошибка
Большинство калькуляторов используют метод проб и ошибок, чтобы найти кубический корень. Метод проб и ошибок хорошо работает для идеальных кубиков. Для несовершенных кубов это может занять очень много времени из-за большого количества десятичных знаков.
Чтобы найти кубированный корень методом проб и ошибок:
- Угадайте число, которое, по вашему мнению, может быть кубическим корнем
- Умножьте число x число x число.
- Если результат слишком низкий, угадайте другое большее число. Если результат слишком высокий, угадайте другое меньшее число.
- Продолжайте повторять, пока не найдете кубический корень.
Пример. Методом проб и ошибок найти кубический корень из 512:
- Попробуйте число — 5: 5 x 5 x 5 = 125 (слишком мало)
- Попробуйте число больше 5-10-10-10 x 10 x 10 = 1000 (слишком большое)
- Попробуйте число от 5 и 10-8-8 x 8 x 8 = 512 (ответ)
Метод 2 — Быстрое нахождение корней из чисел идеального куба
Этот метод позволяет быстрее найти корень идеального числа куба.Однако, если число не является числом идеального кубического корня, этот метод не даст ответа.
Как набрать кубический корень?
- На клавиатуре Windows введите 3. Выберите число и параметр «шрифт» в своей программе и установите для шрифта 3 значение «надстрочный». Затем откройте карту символов, найдите символ квадратного корня и скопируйте / вставьте его в документ.
- На клавиатуре Mac введите 3. Выберите число и параметр «шрифт» в своей программе, а также установите для шрифта 3 значение «надстрочный.Затем нажмите option + v для символа квадратного корня.
- В HTML или веб-документе заключите «3» в теги ( 3 ). После 3 используйте символ квадратного корня √.
Таблица чисел кубического корня — Perfect Cubes
- 3 √1 = 1, как 1 x 1 x 1 = 1
- 3 √8 = 2, как 2 x 2 x 2 = 8
- 3 √27 = 3, как 3 x 3 x 3 = 27
- 3 √64 = 4, поскольку 4 x 4 x 4 = 64
- 3 √125 = 5, поскольку 5 x 5 x 5 = 125
- 3 √216 = 6, как 6 x 6 x 6 = 216
- 3 √343 = 7, как 7 x 7 x 7 = 343
- 3 √512 = 8, как 8 x 8 x 8 = 4096
- 3 √ 729 = 9, поскольку 9 x 9 x 9 = 729
- 3 √1000 = 10, поскольку 10 x 10 x 10 = 1000
- 3 √1331 = 11, поскольку 11 x 11 x 11 = 1,331
- 3 √1728 = 12, поскольку 12 x 12 x 12 = 1,728
- 3 √3375 = 15, поскольку 15 x 15 x 15 = 3,375
- 3 √4913 = 17, как 17 x 17 x 17 = 4,913
- 3 √8000 = 20, поскольку 20 x 20 x 20 = 8000
- 3 √15625 = 25, поскольку 25 x 25 x 25 = 15,625
- 3 √27000 = 30, как 30 Икс 30 x 30 = 27000
- 3 √35936 = 33, так как 33 x 33 x 33 = 35,936
- 3 √ = 45, так как 45 x 45 x 45 = 91,125
- 3 √125000 = 50 , как 50 x 50 x 50 = 125 000
- 3 √216000 = 60, как 60 x 60 x 60 = 216 000
- 3 √421875 = 75, как 75 x 75 x 75 = 421 875
- 3 √1000000 = 100, так как 100 x 100 x 100 = 1000000
Таблица кубических корневых номеров
Обратите внимание: для работы этой таблицы требуется JavaScript. 3- (27) = 0
Пошаговое решение:
Шаг 1:
Попытка учесть разность кубов:
1.1 Факторинг: x 3 -27
Теория: разница двух идеальных кубов, a 3 — b 3 может быть разложена на
(ab) • (a 2 + ab + b 2 )
Доказательство: (ab) • (a 2 + ab + b 2 ) =
a 3 + a 2 b + ab 2 -ba 2 -b 2 ab 3 =
a 3 + (a 2 b-ba 2 ) + (ab 2 -b 2 a) -b 3 =
a 3 + 0 + 0 -b 3 =
a 3 -b 3
Проверка: 27 — куб 3
Проверка: x 3 — куб x 1
Факторизация:
(x — 3) • (x 2 + 3x + 9)
Попытка разложить на множители путем разделения среднего члена
1.2 Факторинг x 2 + 3x + 9
Первый член равен x 2 , его коэффициент равен 1.
Средний член + 3x, его коэффициент равен 3.
Последний член, «константа», равен +9
Шаг-1: Умножьте коэффициент первого члена на константу 1 • 9 = 9
Шаг-2: Найдите два множителя 9, сумма которых равна коэффициенту среднего члена, который равен 3.
| -9 | + | -1 | = | -10 | |||||||||||||||||||||||||
| -3 | + | -3 06 | | -1 | + | -9 | = | -10 | | | 1 | + | 9 | = | | | + | 3 | = | 6 | | | 9 | + | 1 | = | 10 | | |
Два таких фактора могут быть найдены:
Заключение: Трехчлен не может быть разложен на множители
Уравнение в конце шага 1:
(x - 3) • (x 2 + 3x + 9) = 0
Шаг 2:
Теория — Корни продукта:
2.1 Произведение нескольких членов равно нулю.
Если произведение двух или более членов равно нулю, то хотя бы одно из членов должно быть равно нулю.
Теперь мы решим каждый член = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов есть в продукте
Любое решение для члена = 0 также решает продукт = 0.
Решение уравнения с одной переменной:
2.2 Решите: x-3 = 0
Добавьте 3 к обеим сторонам уравнения:
x = 3
Парабола, поиск вершины:
2.3 Найдите вершину y = x 2 + 3x + 9
Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола открывается и, соответственно, имеет самую низкую точку (также известную как абсолютный минимум). Мы знаем это даже до того, как нанесли «y», потому что коэффициент первого члена, 1, положительный (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух x-точек пересечения (корней или решений) параболы.То есть, если парабола действительно имеет два реальных решения.
Параболы могут моделировать множество реальных жизненных ситуаций, например высоту над землей объекта, брошенного вверх через некоторый промежуток времени. Вершина параболы может предоставить нам информацию, например, максимальную высоту, которую может достичь объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы Ax 2 + Bx + C координата x вершины задается как -B / (2A).В нашем случае координата x равна -1,5000
Подставив в формулу параболы -1,5000 для x, мы можем вычислить координату y:
y = 1,0 * -1,50 * -1,50 + 3,0 * -1,50 + 9,0
или y = 6,750
Парабола, графическая вершина и пересечения по оси X:
Корневой график для: y = x 2 + 3x + 9
Ось симметрии (пунктирная линия) {x} = {- 1,50}
Вершина в точке {x, y} = {-1,50, 6,75}
Функция не имеет действительных корней
Решите квадратное уравнение, заполнив квадрат
2.4 Решение x 2 + 3x + 9 = 0, завершив Квадрат.
Вычтем 9 из обеих частей уравнения:
x 2 + 3x = -9
Теперь умный бит: возьмите коэффициент при x, равный 3, разделите его на два, получив 3/2 и, наконец, возведите в квадрат. это дает 9/4
Добавьте 9/4 к обеим частям уравнения:
В правой части мы имеем:
-9 + 9/4 или, (-9/1) + (9/4)
общий знаменатель двух дробей равен 4. Сложение (-36/4) + (9/4) дает -27/4
Таким образом, сложив обе части, мы, наконец, получаем:
x 2 + 3x + (9/4) = — 27/4
Добавление 9/4 завершило левую часть в полный квадрат:
x 2 + 3x + (9/4) =
(x + (3/2)) • (x + (3/2) ) =
(x + (3/2)) 2
Вещи, которые равны одному и тому же, также равны друг другу.Так как
x 2 + 3x + (9/4) = -27/4 и
x 2 + 3x + (9/4) = (x + (3/2)) 2
то по закону транзитивности,
(x + (3/2)) 2 = -27/4
Мы будем называть это уравнение уравнением. # 2.4.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(x + (3/2)) 2 равен
(x + (3/2)) 2/2 =
(x + (3/2)) 1 =
x + (3/2)
Теперь, применяя принцип квадратного корня к уравнению.# 2.4.1 получаем:
x + (3/2) = √ -27/4
Вычтем 3/2 с обеих сторон, чтобы получить:
x = -3/2 + √ -27/4
В математике, i называется мнимой единицей. Он удовлетворяет i 2 = -1. Оба i и -i являются квадратными корнями из -1
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное
x 2 + 3x + 9 = 0
имеет два решения:
x = -3 / 2 + √ 27/4 • i
или
x = -3/2 — √ 27/4 • i
Обратите внимание, что √ 27/4 можно записать как
√ 27 / √ 4, что составляет √ 27/2
Решите квадратное уравнение через квадратную формулу
2.5 Решение x 2 + 3x + 9 = 0 по квадратичной формуле.
Согласно квадратичной формуле, x, решение для Ax 2 + Bx + C = 0, где A, B и C — числа, часто называемые коэффициентами, определяется по формуле:
— B ± √ B 2 -4AC
x = ————————
2A
В нашем случае A = 1
B = 3
C = 9
Соответственно B 2 — 4AC =
9 — 36 =
-27
Применение формулы корней квадратного уравнения:
-3 ± √ -27
x = ——————
2
В наборе действительных чисел отрицательные числа не имеют квадратных корней.Был изобретен новый набор чисел, названный комплексным, чтобы отрицательные числа имели квадратный корень. Эти числа записываются (a + b * i)
Оба i и -i являются квадратными корнями из минус 1
Соответственно √ -27 =
√ 27 • (-1) =
√ 27 • √ -1 =
± √ 27 • i
Можно ли упростить √ 27?
Да! Разложение на простые множители 27 равно
3 • 3 • 3
Чтобы иметь возможность удалить что-либо из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат i.е. второй корень).
√ 27 = √ 3 • 3 • 3 =
± 3 • √ 3
√ 3, округленное до 4 десятичных цифр, составляет 1,7321
Итак, теперь мы смотрим на:
x = (-3 ± 3 • 1,732 i ) / 2
Два мнимых решения:
x = (- 3 + √-27) / 2 = (- 3 + 3i√ 3) / 2 = -1,5000 + 2,5981i или:
x = (- 3-√-27) / 2 = (- 3-3i√ 3) / 2 = -1,5000-2,5981i
Было найдено три решения:
- x = (- 3-√-27) / 2 = (- 3-3i√ 3) / 2 = -1.5000-2.5981i
- x = (- 3 + √-27) / 2 = (- 3 + 3i√ 3) / 2 = -1.5000 + 2.5981i
- x = 3
Факторизация суммы или разности кубов
8.5 — Факторинг суммы или разницы кубиков
8.5 — Факторинг суммы или разницы кубов
Как следует из названий, сумма кубиков является выражением формы:
а разница кубиков — это выражение вида:
Сумму кубиков можно разложить на множители следующим образом:
а разницу кубиков можно разложить на множители следующим образом:
Обратите внимание на знаки, показанные красным. Бином справа имеет такой же знак |
Вы можете легко проверить оба этих фактора, умножив правые части
и заметив, что все условия, кроме условий куба, отменяются.
Вот несколько примеров. В каждом случае мы узнаем форму
а 3 ± б 3 ,
(± — это сокращение от « плюс-минус »),
затем определите a и b , а затем просто укажите факторизованную форму.
Пример: Фактор x 3 + 27.
- Думайте о 27 как о 3 3 .
Тогда это сумма кубиков, и мы можем применить формулу суммы кубов:a 3 + b 3 =
( a + b ) ( a 2 — a b +
б 2 ). - Подстановка a = x и b = 3 в формулу дает:
x 3 + 27 =
( x + 3) ( x 2 — 3 x + 9).
Пример: Фактор 8 x 6 -64 y 3 .
- Представьте 8 x 6 как (2 x 2 ) 3
и 64 y 3 как (4 y ) 3 .
Тогда это разница кубиков, и мы можем применить разницу кубов
формула:a 3 — b 3 =
( a — b ) ( a 2 + a b +
б 2 ). - Замена на = 2 x 2 и
b = 4 y в формулу дает:8 x 6 — 64 y 3 =
(2 x 2 -4 y )
(4 x 4 + 8 x 2 y
+ 16 и 2 ).
Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Специальный факторинг: суммы и разности кубов и идеальные квадраты
Purplemath
Две другие специальные формулы факторизации, которые вам нужно запомнить, очень похожи друг на друга; это формулы для разложения сумм и разностей кубов. Вот две формулы:
Факторинг суммы кубов:
a 3 + b 3 = ( a + b ) ( a 2 — ab + b 2 )
Фактор разницы кубов:
a 3 — b 3 = ( a — b ) ( a 2 + ab + b 2 )
На более продвинутых курсах вы узнаете, как они пришли к этим формулам.А пока просто запомните их.
MathHelp.com
Чтобы облегчить запоминание, сначала обратите внимание, что членов в каждой из двух формул факторизации абсолютно одинаковы.Затем обратите внимание, что каждая формула имеет только один знак «минус». Разница между этими двумя формулами заключается в расположении одного знака «минус»:
Для разности кубов знак «минус» идет в линейном множителе, a — b ; для суммы кубиков знак «минус» стоит в квадратичном множителе, a 2 — ab + b 2 .
Некоторые люди используют мнемонику « SOAP », чтобы отслеживать знаки; буквы обозначают линейный множитель, имеющий «тот же» знак, что и знак в середине исходного выражения, затем квадратичный множитель, начинающийся со «противоположного» знака того, что было в исходном выражении, и, наконец, второй знак внутри квадратичный множитель «всегда положителен».
a 3 ± b 3 = ( a [ Тот же знак ] b ) ( a 2 [ Противоположный знак ] ab [ Всегда Положительный ] b 2 )
Какой бы метод лучше всего ни помог вам сохранить эти формулы, используйте его, потому что вы не должны предполагать, что вам будут даны эти формулы на тесте.Вы должны ожидать, что вам нужно будет их знать.
Примечание. Квадратичная часть каждой формулы куба не учитывает множитель , поэтому не тратьте время на попытки разложить его на множители. Да, a 2 — 2 ab + b 2 и a 2 + 2 ab + b 2 Коэффициент , но это из-за двойки в середине условия. Квадратичные члены этих формул суммы и разности кубов не содержат , равного «2», и, таким образом, не может множить .
Когда вам дается пара кубиков для факторизации, внимательно примените соответствующее правило. Под «осторожно» я имею в виду «использование круглых скобок для отслеживания всего, особенно отрицательных знаков». Вот несколько типичных проблем:
Это эквивалентно x 3 -2 3 . Со знаком «минус» посередине это разница кубиков. Для факторинга я подставлю x и 2 в формулу разности кубов.Так я получаю:
x 3 — 8 = x 3 -2 3
= ( x — 2) ( x 2 + 2 x + 2 2 )
= ( x — 2) ( x 2 + 2 x + 4)
Первый член содержит куб 3 и куб x .А как насчет второго срока?
Прежде чем паниковать по поводу отсутствия кажущегося куба, я помню, что 1 можно рассматривать как возведенную в любую степень, которая мне нравится, поскольку 1 для любой степени по-прежнему равна 1. В этом случае мне нужна степень 3, так как это даст мне сумму кубиков. Это означает, что выражение, которое они мне дали, может быть выражено как:
Итак, чтобы разложить множители, я подставлю 3 x и 1 в формулу суммы кубов.Это дает мне:
27 x 3 + 1 = (3 x ) 3 + 1 3
= (3 x + 1) ((3 x ) 2 — (3 x ) (1) + 1 2 )
= (3 x + 1) (9 x 2 — 3 x + 1)
Во-первых, я отмечаю, что они дали мне бином (двухчленный многочлен) и что мощность x в первом члене равна 3, поэтому, даже если я не работал с «суммами и разностями» кубиков »моего учебника, я бы заметил, что, возможно, мне следует думать в терминах этих формул.
Глядя на другую переменную, я замечаю, что степень 6 — это куб степени 2, поэтому другая переменная в первом члене также может быть выражена в кубе; а именно, как куб квадрата у .
Второй член — 64, который, как я помню, является кубом 4. (Если бы я не вспомнил или не был уверен, я бы взял свой калькулятор и пробовал вычислять кубики, пока не получил правильное значение. , иначе я бы взял кубический корень из 64.)
Итак, теперь я знаю, что с минусом в середине это разница в два куба; а именно это:
Подставляя подходящую формулу, я получаю:
x 3 y 6 — 64 = ( xy 2 ) 3 — 4 3
= ( xy 2 -4) (( xy 2 ) 2 + ( xy 2 ) (4) + 4 2 )
= ( xy 2 -4) ( x 2 y 4 + 4 xy 2 + 16)
Используя соответствующую формулу, множите 16
x 3 — 250.
Гм … Я знаю, что 16 — это , а не куб чего-либо; на самом деле он равен 2 4 . Как дела?
Что случилось, так это то, что они ожидают, что я использую то, что я узнал о простом факторинге, чтобы сначала преобразовать это в разность кубов. Да, 16 = 2 4 , но 8 = 2 3 , куб. Я могу получить 8 из 16, разделив на 2.Что будет, если я разделю 250 на 2? Я получаю 125, что является кубом из 5. То, что они мне дали, можно переформулировать как:
Я могу применить формулу разности кубов к тому, что находится в круглых скобках:
2 3 x 3 — 5 3 = (2 x ) 3 — (5) 3
= (2 x — 5) ((2 x ) 2 + (2 x ) (5) + (5) 2 )
= (2 x — 5) (4 x 2 + 10 x + 25)
Собирая все вместе, я получаю окончательную факторизованную форму:
2 (2 x -5) (4 x 2 + 10 x + 25)
Моей первой реакцией могло бы стать применение формулы разности кубов, поскольку 125 = 5 3 .Но как насчет того знака «минус» впереди?
Поскольку ни одна из приведенных мне формул факторинга не включает в себя «минус» впереди, может быть, я смогу вычесть «минус» …?
— x 3 — 125 = –1 x 3 — 125
Ага! Теперь то, что внутри скобок — это сумма кубов, которую я могу разложить на множители. У меня есть сумма куба x и куба 5, поэтому:
x 3 + 5 3 = ( x + 5) (( x ) 2 — ( x ) (5) + (5) 2 )
= ( x + 5) ( x 2 -5 x + 25)
Собирая все вместе, получаем:
–1 ( x + 5) ( x 2 — 5 x + 25)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении суммы кубов.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления .)
URL: https://www.purplemath.com/modules/specfact2.htm
Кубический корень — это то же самое, что возвести в степень 1/3?
Недавно я обнаружил интересное несоответствие, связанное с функцией кубического корня.
Кубический корень
В Wolfram | Alpha (который использует систему компьютерной алгебры Mathematica в своей бэкэнд), если вы попросите его построить график, вы получите следующее, как и ожидалось:
В поле поиска я ввел «кубический корень из x», и он сказал, что «Результат» был правильно написан как.
Этот график является отражением графика y = x 3 в линии y = x . Это обратные функции.
Мы знаем, что кубический корень отрицательного числа отрицательный, поэтому, например, мы можем видеть, что это имеет смысл на графике выше.
Wolfram | Alpha утверждает, что существует один корень ( x = 0), а домен и диапазон — все действительные числа, что согласуется с приведенным выше графиком.
ПРИМЕЧАНИЕ: Крошечным шрифтом, Wolfram | Alpha указывает:
Предположим, что «кубический корень из» является корнем с действительным знаком.
Есть возможность увидеть «основной корень», но это дало тот же результат.
Возведение в степень 1/3
На ранних этапах изучения корней и дробных степеней мы узнаем, что можем записать корни в дробных показателях.В общем, это означает:
Итак, для квадратного корня мы имеем:
и для кубического корня:
.
Таким образом, мы ожидаем, что график будет таким же, как и график для.
Но это не так. Вот что возвращает Wolfram | Alpha, когда я прошу его построить график:
Синяя кривая обозначена как «действительная часть», а красная кривая — «мнимая часть».
Любопытно, что значение «Input» указано как:, но на самом деле это не то, что я ввел.Итак, часть ответа касается, а остальная часть ответа — нет.
Из раздела, посвященного комплексным корням (особенно см. Упражнение 4 в конце), мы знаем, что кубическое уравнение будет иметь 3 корня (точно так же, как квадратное уравнение имеет 2 корня). Все эти 3 корня могут быть настоящими или смесью реальных и сложных корней.
Wolfram | Alpha правильно указывает, что есть мнимые части, но верен ли их график? Неужели кубический корень отрицательного числа должен быть отрицательным?
Пример: Каковы все кубические корни из −8?
Я немного уменьшил масштаб, чтобы получить этот график, и добавил несколько направляющих сегментов (зеленых):
Используя те же соображения, что и в упражнении 4, упомянутом ранее, комплексные решения для x 3 = −8 должны находиться на расстоянии 120 ° друг от друга, что дает (где):
х = −2
х = 1 + 1.73j
x = 1 — 1.73j
Приведенный выше график действительно дает нам одно из этих решений (среднее, поскольку мы видим, что действительная часть равна 1, а мнимая часть — 1,73), но не дает двух других решений.
Еще раз, страница сообщает нам, что принимает «основной корень», и дает нам возможность выбрать «действительный корень». Если мы сделаем это на этот раз, мы получим настоящую корневую версию, похожую на график в верхней части страницы.
Научная тетрадь ответ
Scientific Notebook дает следующие 2 графика, которые я наложил.
Синий график показывает, и Scientific Notebook дает полное реальное решение (в первом и третьем квадрантах), тогда как пурпурный (розовый) график находится только в положительном квадранте.
Геогебра и Десмос ответы
И Geogebra, и Desmos дают один и тот же график «полного реального значения» для обоих и.
Аналогично квадратному корню
Я уже писал о количестве решений для √16.



 a * (a — b) + b * (a — b) = (a — b) * (a + b)
a * (a — b) + b * (a — b) = (a — b) * (a + b)